Ein Würfel
Ein Objekt meiner Bewunderung war immer wieder dieser Würfel (Abb. 15.1).

Abb. 15.1: Pieros Würfel, fig. LIV (Piero della Francesca 1942, Tav. XXIX)
Was ist denn Besonderes daran? Piero della Francesca, ein Maler, verfasst für Maler ein Lehrbuch über Zentralperspektive und zeigt hier das perspektive Bild eines Würfels (Piero della Francesca 1899, 1942, 1984).
Irgendeines Würfels? Ja, irgendeines Würfels. Der Würfel steht nicht in Frontalperspektive vor uns, nicht mit seiner Unterseite platt auf einer Standebene, nicht mit seiner Vorder- und Hinterseite parallel zur Bildebene, aber auch nicht gedreht, in Übereckperspektive. Dieser Würfel steht auf einer seiner acht Ecken, auf einer Spitze, und keine Kante hat eine ausgezeichnete Richtung, weder parallel zur Standebene noch parallel zur Bildebene. Wir haben das perspektive Bild eines Würfels in allgemeiner Lage vor uns.
In der Wirklichkeit stehen Würfel im Allgemeinen nicht auf einer Ecke. Auch keine Bauwerke. Niemals wird ein Maler einen Würfel in allgemeiner Lage zeichnen müssen, wenn er reale Welten in seinen Bildern vorzeigen will.
Und ist es wirklich ein perspektives Bild? Es gibt weder Horizont noch Hauptpunkt, keine Fluchtpunkte, keine Diagonal- oder Messpunkte.
Der Würfel auf der Spitze in Grund- und Aufriss
Stellen wir die Frage nach der Perspektive zurück. Es ist nicht die Perspektivkonstruktion, die meine Aufmerksamkeit erregt hat. Aber der fast zwanghafte Blick auf die Perspektive hat wohl verhindert, dass die zwei kleinen Schritte, die ihr vorausgehen, von der Fachwelt überhaupt bemerkt wurden. Diese beiden Schritte jedoch sind die eigentliche Sensation. Das wirklich Besondere in Pieros „De Prospectiva Pingendi“ kommt eher nebensächlich daher. Es ist die geometrisch exakte Konstruktion des Würfels in allgemeiner Lage als Voraussetzung für seine perspektive Abbildung. Es ist die Figur LII (Piero della Francesca 1942, Tav. XXVIII), die ich zum besseren Verständnis in nachkonstruierten Einzelschritten vorführen werde. Wie aus dem Nichts haben wir hier nicht nur die maßgenaue geometrische Definition eines Körpers durch seinen Grund- und Aufriss, sondern diese Risse werden souverän benutzt, um zu einer Lagedefinition des Würfels zu kommen, die man anders nicht erreichen könnte. Und noch dazu eine geometrische Lage, wie sie der Würfel niemals annehmen könnte – auf einer Spitze stehend, irgendwie, eine Inszenierung.
Folgen wir diesen ersten Konstruktionsschritten Piero della Francescas. Es gibt im Prinzip nur einen Weg, und Piero geht ihn. Vorläufer, auf denen er hätte aufbauen können, kennen wir nicht (vgl. Lefèvre 2004). Erst Monge (1989) wird diesen Weg systematisch entwickeln. Es ist der Weg über zugeordnete Risse: Ordner, also „Verbindungsgeraden“, gestatten Projektionen von einem Riss in den anderen, vom Grundriss in den Aufriss und umgekehrt, und ermöglichen so die schrittweise und verlustfreie Verwandlung des Würfels in den Würfel auf der Spitze.
Piero beginnt im Grundriss mit dem übereck gedrehten, auf der Standebene liegenden Würfel und seinem durch orthogonale Ordner in die Aufrissebene bestimmten Aufriss (Abb. 15.2).
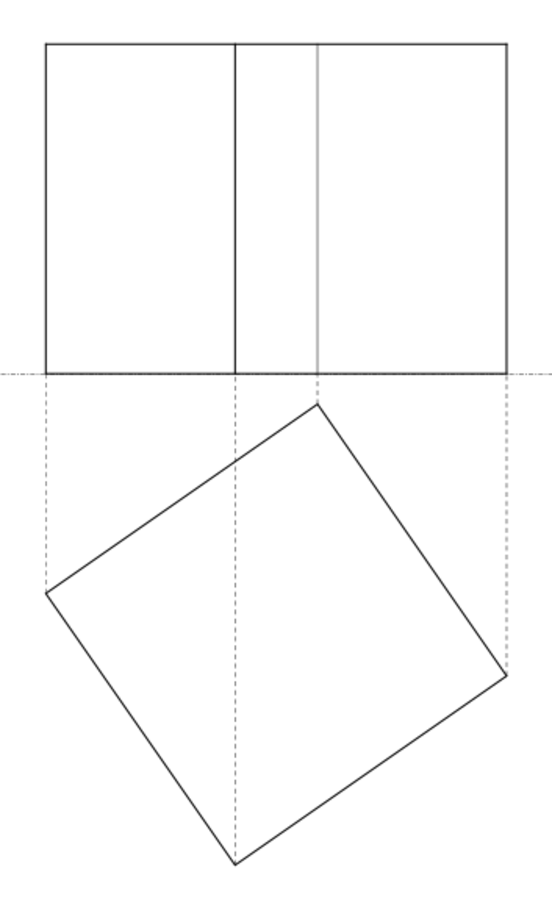
Abb. 15.2: Der Würfel in Übereck-Ansicht in Grund- und Aufriss (nach Piero, fig. LII, Piero della Francesca 1942, Tav. XXVIII)
Im nächsten Schritt dreht er den Würfel im Aufriss so, dass er auf der Ecke F zu stehen kommt. Dabei bewegen sich im Grundriss die Ecken auf Ordnern parallel zur Rissachse, der Schnittgeraden von Grund- und Aufrissebene, und durch den Schnitt dieser Ordner mit den Loten aus den Ecken des Würfels im Aufriss gewinnt er die Ecken des auf der Spitze stehenden Würfels im Grundriss (Abb. 15.3).
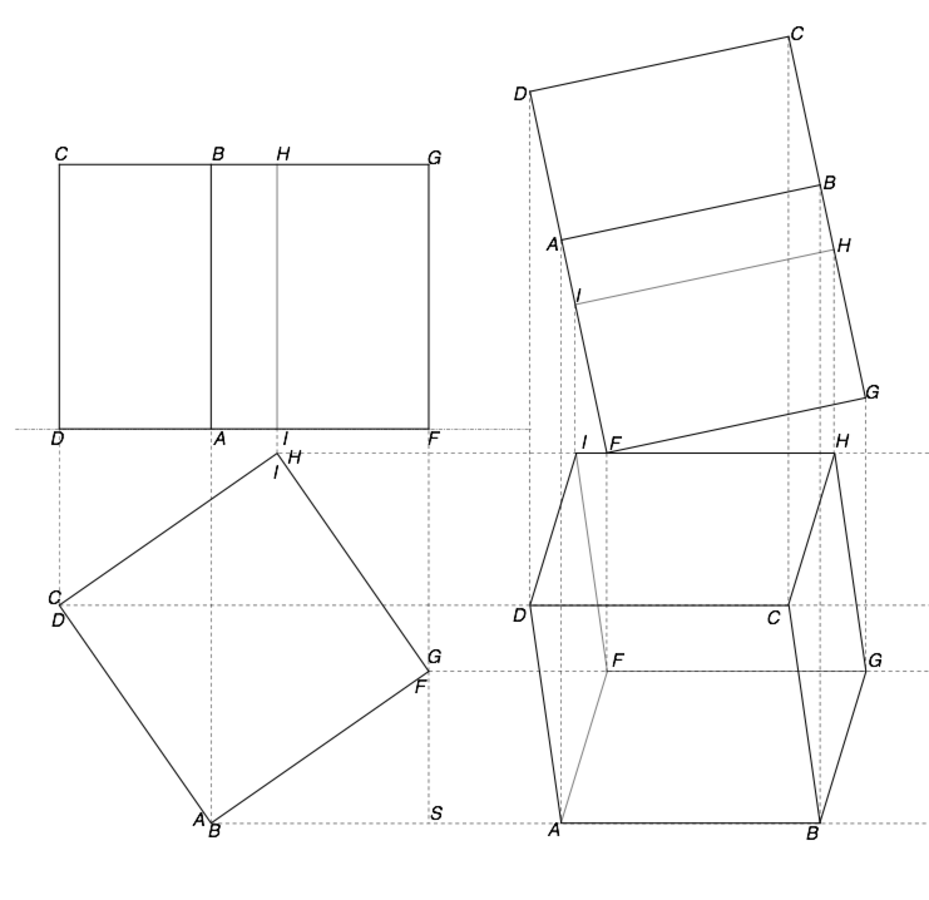
Abb. 15.3: Der im Aufriss auf eine Ecke gedrehte Würfel im Aufriss und Grundriss (nach Piero, fig. LII, Piero della Francesca 1942, Tav. XXVIII)
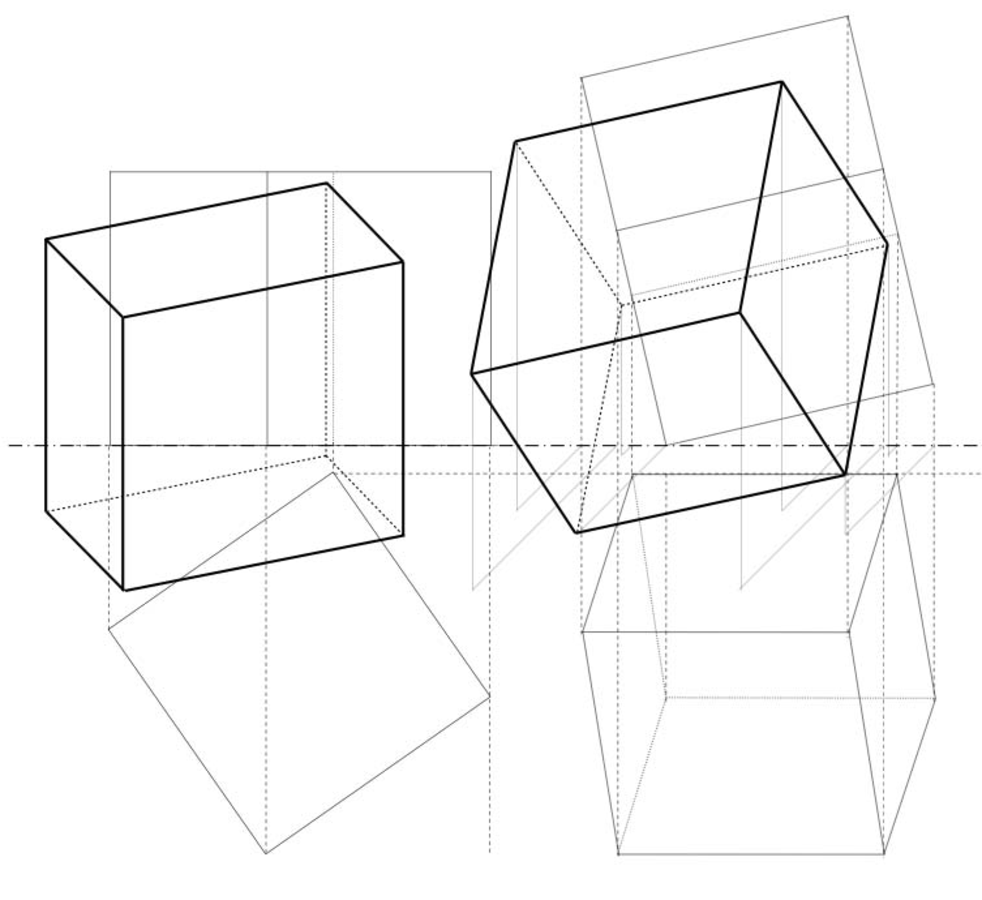
Damit ist der Würfel in allgemeiner Lage konstruktiv und messgenau in Grundriss und Aufriss bestimmt. In Abb. 15.4 sind beide Würfelpositionen, also der Transformationsschritt vom in Übereckposition liegenden in den auf einer Ecke stehenden Würfel von mir zusätzlich in Kavaliersperspektive veranschaulicht. So bändigt er diese flüchtige Form und erkundet, wie der Würfel Gestalt annimmt, während er ihn mit mathematischen Mitteln zeichnend auf eine Ecke stellt.
Exkurs: Die perspektive Abbildung über Grund- und Aufriss des visuellen Systems
Offenbar braucht Piero den Würfel in allgemeiner Lage, also einen besonders schwierigen Körper, als Vorwand, um eine andere Methode der perspektiven Konstruktion als notwendig erscheinen zu lassen: „[...] deshalb werde ich, da ich von schwierigern Körpern zu handeln habe, einen andern Weg und eine andere Methode bei ihren Verkürzungen einschlagen [...]“ (Winterberg 1899, Bd. 1, CXXV).1
Eine andere Methode als welche? Als die Albertis natürlich, deren Begründung und Weiterentwicklung Piero die beiden ersten seiner drei Teile umfassenden Abhandlung „De Prospectiva Pingendi“ widmet. Es ist Alberti, der durch die Konstruktion des Diagonalpunkts auf dem Horizont im gleichen Abstand vom Hauptpunkt wie der des Betrachters vom Bild das Auge des Betrachters mit der Zeichnung verknüpft. Und der Versuch Pieros, Albertis Verfahren und sein eigenes, entwickelteres, aber im Prinzip äquivalentes Verfahren am Beispiel der Abbildungs eines Quadrats mathematisch über Strahlensätze zu beweisen (Abb. 15.5), wäre eine weitere kleine Untersuchung wert.

Abb. 15.5: Piero fig. XIII (Piero della Francesca 1942, Tav. IV)
Für die perspektive Darstellung der geschreinerten Welt in Frontal- bzw. Übereckperspektive mag Albertis oder Pieros Verfahren über Horizont, Hauptpunkt und Diagonalpunkte als Messpunkte für die Diagonalen reichen, doch nicht für die „schwierigeren Körper“.
Moritz Cantor findet eine operative Definition für das perspektive Bild, nämlich als „[...] die Kunstfertigkeit, die zu bemalende Wand als zwischen dem sehenden Auge und dem abzubildenden Gegenstande eingeschaltet zu denken und deren Durchschnittspunkte mit den Sehstrahlen nach jenem Gegenstande durch Linien zu vereinigen“ (Cantor 1880, 67). In fig. XLV (Abb. 15.6) zeigt Piero seinen anderen Weg, der wie eine konstruktive Umsetzung der anschaulichen Beschreibung Cantors daherkommt, indem er dieses visuelle System aus Auge, Sehstrahlen, Bildebene und Quadrat in Grund- und Aufriss zerlegt. Im Grundriss gewinnt er die horizontalen Koordinaten der vier benötigten Durchschnittspunkte der entsprechenden Sehstrahlen und analog im Seitenriss ihre Höhen. Mit diesen beiden Maßangaben sind die vier Bildpunkte in der Bildebene eindeutig bestimmt. Piero überträgt sie in einer eigenen Zeichnung (Abb. 15.6 unten), indem er sie auf Papierstreifen aufträgt und dann jeweils Weite und Höhe (larghezza und altezza) eines Punkts zum Schnitt bringt und die Bildpunkte zum Bild des Quadrats verbindet.
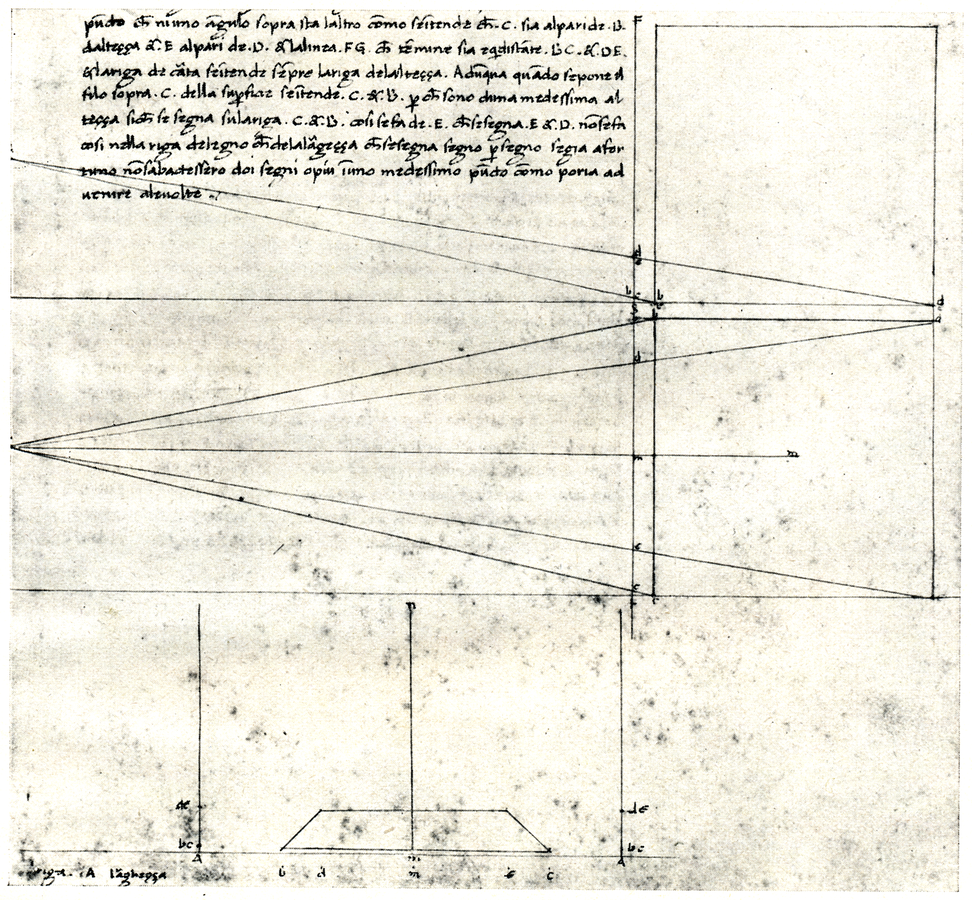
Abb. 15.6: Piero fig. XIII (Piero della Francesca 1942, Tav. IV)
Der Würfel auf der Spitze in perspektiver Abbildung
Gestützt auf diesen Exkurs können wir die perspektive Abbildung des Würfels in allgemeiner Lage mit Pieros Hilfe vollenden. Ein geeignetes visuelles System muss bestimmt und mit Grund- und Aufriss des Würfels verbunden werden. Piero wählt die Gerade KL (Abb. 15.7) als Grundriss der senkrechten Bildebene so, dass keine Kante des Würfels zu ihr parallel liegt, und setzt das Projektionszentrum O „[...] soweit als du entfernt stehen willst, um den Cubus zu sehen.“ Die Projektionsstrahlen von O zu den Ecken des Würfels bestimmen auf KL die horizontalen Koordinaten ihrer Bildpunkte. Bei Piero wird ein Holzstreifen an KL angelegt – „dass er gut fest liege“ – und ein Faden von O nacheinander zu den Würfelecken gespannt und die Schnitte mit dem Holzstreifen auf diesem vermerkt.
Fehlt uns noch das visuelle System im Seitenriss. Das gewinnt Piero durch zugeordnete Risse (Abb. 15.8). Zur Bildebene KL zieht er eine senkrechte Gerade als Rissachse, die KL im Punkt E schneidet, so dass der Abschnitt KE zum Grundriss und LE zum Seitenriss der Bildebene wird. Den Seitenriss des Würfels findet Piero, indem er auf Parallelen zu KL durch alle Eckpunkte des Würfels im Grundriss von der Rissachse PQ aus ihre Höhen abträgt, die er dem Aufriss vom Anfang (Abb. 15.3) entnimmt, und die so gefundenen Ecken des Würfels verbindet. Das Projektionszentrum ist durch seinen Abstand zur Bildebene im Grundriss bereits bestimmt, seine Höhe wählt er nach Gefallen (Abb. 15.9). Im Seitenriss des visuellen Systems bestimmen die Projektionsstrahlen von O zu den Ecken des Würfels auf KL die Höhen der Bildpunkte über der Standebene, die er wieder auf einem Holzstreifen vermerkt. Die Fertigstellung des perspektiven Bildes des Würfels erfolgt durch Bestimmung der Bildpunkte mit Hilfe der auf den Holzstreifen eingezeichneten Koordinaten (Abb. 15.10).

Abb. 15.7: Das visuelle System im Grundriss, mit Projektionszentrum O, Bildebene KL,Würfel in allgemeiner Lage und Projektionsstrahlen (nach Piero, fig. LII, Piero della Francesca 1942, Tav. XXVIII)

Abb. 15.8: Die Konstruktion des Würfels im Seitenriss in neuer Lage (nach Piero, fig. LIII, Piero della Francesca 1942, Tav. XXIX)

Abb. 15.9: Das visuelle System im Seitenriss (nach Piero, fig. LIII, Piero della Francesca 1942, Tav. XXIX)

Abb. 15.10: Die Konstruktion des perspektiven Bildes (nach Piero, fig. LIV, Piero della Francesca 1942, Tav. XXIX)
Zurück zur Ausgangsfrage: Was ist Besonderes daran?
Die Konstruktion perspektiver Bilder schwieriger Körper über Grund- und Aufriss des visuellen Systems wurde möglicherweise schon von Brunelleschi bei der Herstellung seiner Bilder für sein „Perspektive-Straßentheater“ vor dem Baptisterium und vor dem Palazzo Vecchio in Florenz verwendet. Mit Pieros „De Prospectiva Pingendi“ von etwa 1572–75 haben wir jedenfalls zum ersten Mal den Riesenschritt schriftlich und nachvollziehbar dokumentiert, Albertis Vorstellung des Bildes als Fenster, durch das wir auf die dargestellte Welt schauen, als Schnitt mit der Sehstrahlpyramide in zugeordnetem Grund- und Aufriss geometrisch hervorgehen zu sehen.
Uns verwundert nicht so sehr Pieros Anwendung dieser Methode auf den hier behandelten Würfel, sondern eher auf wirklich schwierige Körper wie den menschlichen Kopf, den er geradezu besessen von der Idee, jeden Körper geometrisch konstruieren zu wollen, in bis zu sieben Scheiben zerlegt, von denen er fast hundert Punkte in Grund- und Aufriss bestimmt, um so das perspektive Bild dieses Kopfes zu gewinnen (Abb. 15.11, 15.12). Diese Vermessung des Kopfes wurde oft unsinnigerweise mit den Verfahren zur digitalen Darstellung des Kopfes verglichen und Piero als Prophet der Digitalisierung organischer Formen gepriesen. Piero zeigt hier, was mit konstruktiver Genauigkeit möglich ist. Ob er es in seiner Malerei etwa bei seinen majestätischen Frauen wie der Madonna del Parto in Monterchi jemals angewendet hat?
Doch Pieros Perspektivkonstruktion eines Würfels in allgemeiner Lage mit Hilfe zugeordneter Risse kommt offensichtlich so überraschend und verfrüht, dass sie lange niemand bemerkte. Vasari weiß es nicht so genau: „Er galt für einen vorzüglichen Meister in schwieriger Zeichnung regelmäßiger Körper und in der Arithmetik und Geometrie, ward aber im Alter von Blindheit und endlich durch den Tod verhindert, seine künstlerischen Anstrengungen zu nützen und seine vielen Bücher herauszugeben, welche noch in Borgo, seiner Vaterstadt, aufbewahrt werden.“ Und an anderer Stelle: „Piero war, wie ich schon sagte, sehr eifrig im Studium der Kunst, beschäftigte sich viel mit Perspektive und war wohl bewandert im Euklid, so daß er die wichtigsten Kreislinien regelmäßiger Körper besser als irgend sonst ein Geometer verstand, ja die meisten Aufklärungen haben wir von ihm [...]“ (Vasari 1988, 297). Wiener beschreibt Pieros „De Prospectiva Pingendi“, deren Titel er nicht kennt, als „eine ausgedehnte Schrift mit vielen Figuren“, „die aber jetzt nicht aufgefunden ist“ (Wiener 1884, Bd. 1, 13). Witting zeigt sich sehr gut informiert über die „De Prospectiva Pingendi“, betont die Bedeutung, die dieses Werk über Jahrhunderte als Fundamentalwerk behielt. Er redet aber nur von den ersten beiden Büchern, das dritte mit dem Verfahren der Konstruktion des perspektiven Bildes über Grund- und Aufriss des visuellen Systems erwähnt er nicht, so auch nicht die Konstruktion des Würfels auf der Spitze (Witting 1898, 152ff). Wenn es hochkommt, dann wird die orthogonale Zweitafelprojektion Pieros als „costruzione legittima“ Brunelleschi zugeschrieben, von der dann Piero auf einem geheimnisvollen Wege etwa 30–40 Jahre nach dessen Tode (1446) erfahren hätte (Salmi 1979, 201). Battisti beschränkt sich in seinem umfassenden zweibändigen Werk strikt auf die Malerei von Piero. Immerhin erwähnt er Pieros Konstruktion über Grund- und Aufriss als notwendig für den Fall, dass es etwa Schwierigkeiten bei der perspektivischen Abbildung von geometrischen Objekten komplexer Formen gibt (Battisti 1971, 95).
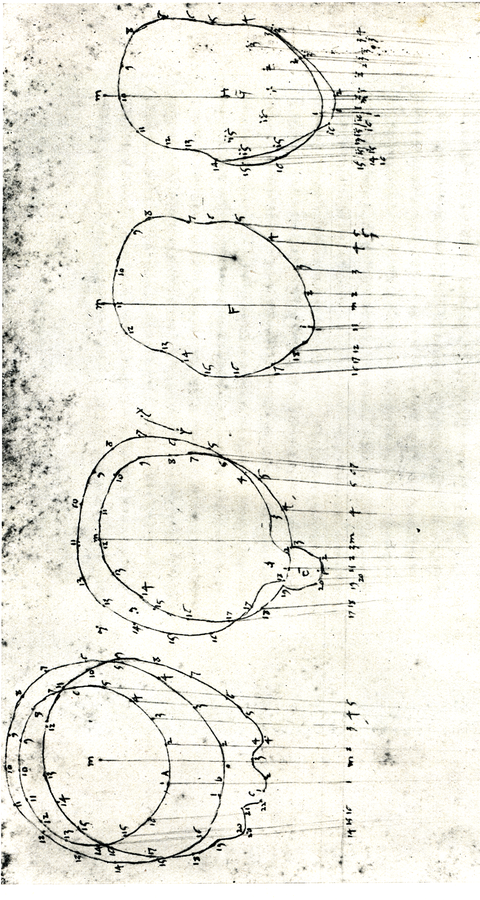
Abb. 15.11: Pieros Zerlegung eines Kopfes in Scheiben (nach Piero, fig. LXX, Piero della Francesca 1942, Tav. XLII)
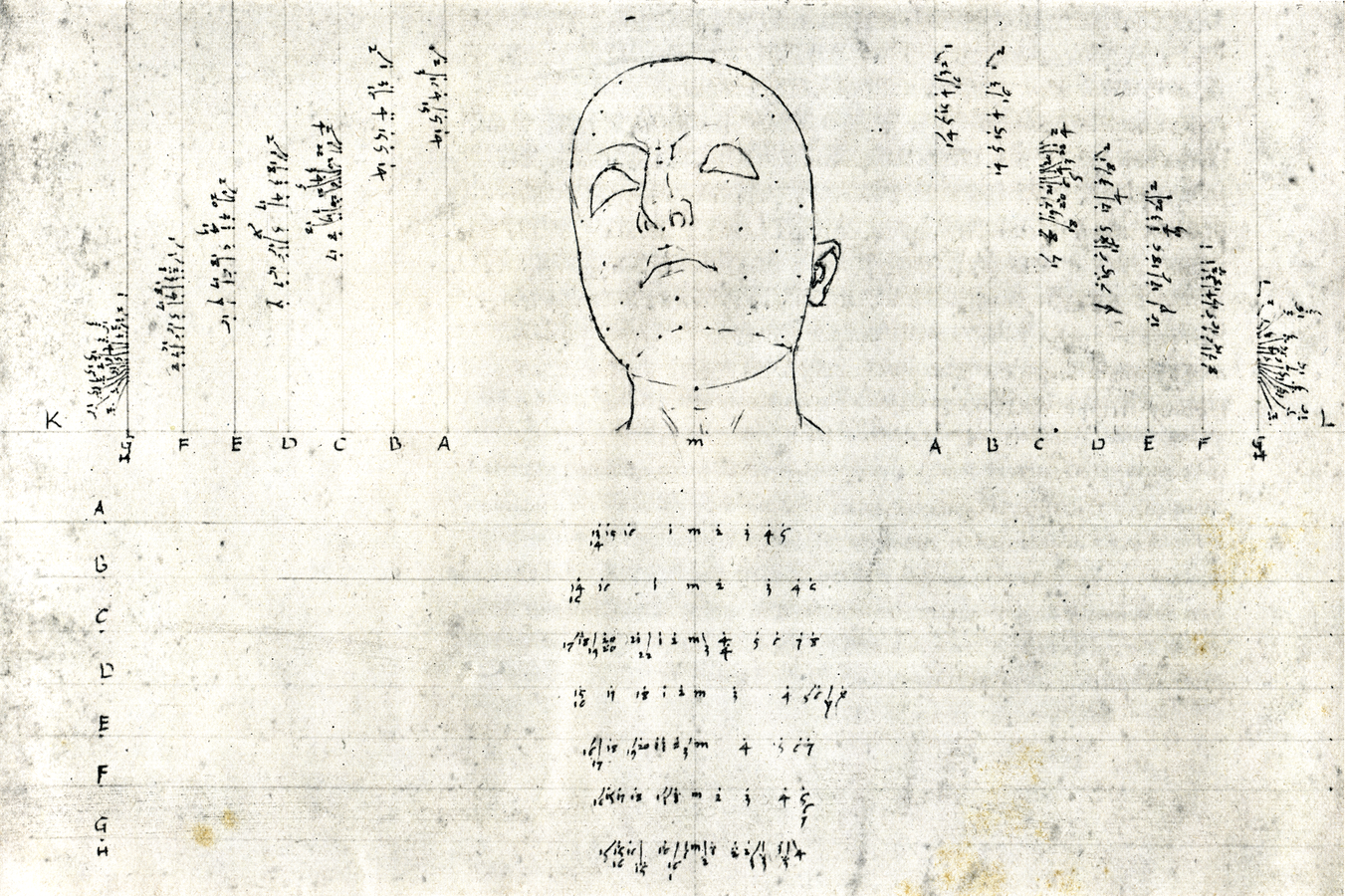
Abb. 15.12: Pieros Konstruktion eines Kopfes aus Scheiben, fig. LXXII (Piero della Francesca 1942, Tav. XLIV)
Insbesondere aber ist es auf Grund der äußerst mageren Quellenlage nicht gelungen, Pieros historisch so überraschende und singuläre meisterhafte Grundrisskonstruktion des Würfels auf der Spitze als Ergebnis einer historischen Genese oder als Reflektion einer schon vorher ausgeübten handwerklichen Technik zu begründen. In der informativen Zusammenstellung architektonischer Skizzen von Joël Sakarovitch (1998), einer umfassenden Recherche zur Genese der Darstellenden Geometrie, finden wir architektonische Grundrisse mesopotamischer und ägyptischer Provenienz, doch keine zugeordneten Risse. Von einer Wiederbelebung griechischer oder römischer Kenntnisse, wie allgemein der Renaissance als Antrieb unterstellt, kann keine Rede sein, denn architektonische Risse aus dieser Zeit sind nicht überliefert. Ansätze etwa bei Villard de Honnecourt (Hahnloser 1935) erreichen nicht einmal die begrenzten Möglichkeiten, wie wir sie am Beispiel (Abb. 15.13) aus der „Geometria Deutsch“ von 1487 von Matthäus Roritzer vor uns haben. Offensichtlich wird Pieros Konstruktion des Würfels auf der Spitze über zugeordnete Risse sogar auch in einschlägigen historischen Untersuchungen einfach übersehen.2 Verstellte etwa die (hier nicht gerechtfertigte) Bewunderung für Dürer, der in diesem Zusammenhang oft genannt wird, den Blick auf diese kleine unschätzbare Kostbarkeit bei Piero?
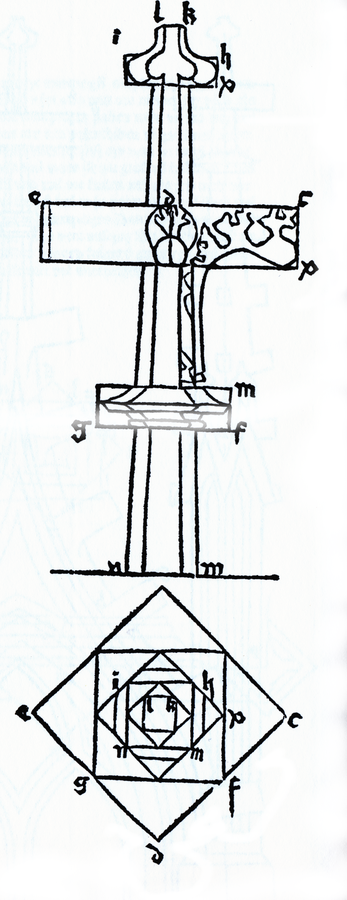
Abb. 15.13: Matthäus Roritzer „Die Geometria Deutsch“, 1487/88 (Roritzer 1999, 42)
Als ich 1986 meinen ersten Vortrag über „Piero della Francesca als Mathematiker“ hielt und Piero als Entdeckung des 20. Jh. vorstellte, mit dem Hinweis auf seine Konstruktion des perspektiven Bildes eines Würfels in allgemeiner Lage über Grund- und Aufriss des visuellen Systems und der Frage, ob er sich hier als früher Vorläufer Monges erweist (Stoller 1990, 25ff), ahnte ich nicht, dass die in dieser Frage herrschende Literaturwüste schon zwei Jahre später durch einen fulminanten Aufsatz von Kirsti Andersen urbar gemacht wurde (Andersen 1992, 2007).
References
Andersen, Kirsti (1992). Perspective and the Plan and Elevation Technique, in Particular in the Work by Piero della Francesca. In: Amphora: Festschrift für Hans Wussing zu seinem 65. Hrsg. von Sergej Demidov. Berlin: Birkhäuser.
– (2007). The Geometry of an Art: The History of the Mathematical Theory of Perspective From Alberti to Monge. New York: Springer.
Battisti, Eugenio (1971). Piero della Francesca. 2 Bde. Milano: Istituto Editoriale Italiano.
Camerota, Filippo (2004). Renaissance Descriptive Geometry: The Codification Of Drawing Methods. In: Picturing Machines 1400–1700. Hrsg. von Wolfgang Lefèvre. Cambridge, London: MIT Press, 175–208.
Cantor, Moritz (1880). Vorlesungen über Geschichte der Mathematik. Erster Band: Von den ältesten Zeiten bis zum Jahre 1200 nach Christi. Leipzig: Teubner.
Field, Judith Veronica (1997). The Invention of Infinity: Mathematics and Art in the Renaissance. Oxford: Oxford University Press.
– (2005). Piero Della Francesca: A Mathematician’s Art. New Haven: Yale University Press.
Grasselli, Luigi (2008). Piero della Francesca, la Matematica et la Prospettiva. In: Piero della Francesca: De Prospectiva Pingendi. Hrsg. von Massimo und Luigi Grasselli Mussini. Sansepolcro: Aboca Museum, 163–269.
Hahnloser, Hans (1935). Villard de Honnecourt. Kritische Gesamtausgabe des Bauhüttenbuches Ms. FR. 19093 der Pariser Nationalbibliothek. Wien: A. Schroll.
Lefèvre, Wolfgang (2004). The Emergence Of Combined Orthographic Projections. In: Picturing Machines 1400–1700. Hrsg. von Wolfgang Lefèvre. Cambridge, London: MIT Press, 209–244.
Loria, Gino (1921). Storia della geometria descrittiva dalle origini sino ai giorni nostri. Mailand: U. Hoepli.
Monge, Gaspard (1989). Geométrie descriptive. Paris, L’an trois de la République (1795). Sceaux: J. Gabay.
Piero della Francesca (1899). Petrus Pictor Burgensis de Prospectiva Pingendi. Hrsg. von Christian Winterberg. 2 Bde. Straßburg: Heitz.
– (1942). De Prospectiva Pingendi. Atlante dei disegni originali. Edizione critica a cura di Giusta Nicco-Fasola. Florenz: G. C. Sansoni.
– (1984). De Prospectiva Pingendi. Edizione critica a cura di Guista Nicco-Fasola con due note di Eugenio Battisti e Franco Ghione ed una bibliografia a cura di Eugenio Battisti e R. Pacciani. Florenz: Le Lettere.
Roritzer, Matthäus (1999). Das Büchlein von der Fialen Gerechtigkeit. Faksimile der Originalausgabe Regensburg 1486. Die Geometria Deutsch. Faksimile der Originalausgabe Regensburg um 1487/88. Hrsg. von Ferdinand Geldner. Hürtgenwald: Pressler.
Sakarovitch, Joël (1998). Épures d’architecture: De la coupe des pierres à la géometrie descriptive. XVIo–XIXo siècles. Basel, Boston, Berlin: Birkhäuser.
Salmi, Mario (1979). La Pittura di Piero della Francesca. Novara: Istituto Geografico De Agostini.
Stoller, Diethelm (1990). Aulis Verlag. In: Mathematikdidaktik, Bildungsgeschichte, Wissenschaftsgeschichte II. Hrsg. von Hans-Georg Steiner. Köln: Werner’sche Verlagsgesellschaft, 17–35.
Vasari, Giorgio (1988). Leben der ausgezeichnetsten Maler, Bildhauer und Baumeister von Cimabue bis zum Jahre 1567. Deutsche Ausgabe von Ludwig Schorn & Ernst Förster, neu herausgegeben & eingeleitet von Julian Kliemann. Nachdruck der ersten deutschen Gesamtausgabe Stuttgart und Tübingen 1832-1849. 2 Bde. Worms: Werner’sche Verlagsgesellschaft.
Wiener, Christian (1884). Lehrbuch der Darstellende Geometrie. 2 Bde. Leipzig: Teubner.
Witting, Felix (1898). Piero dei Franceschi: Eine kunsthistorische Studie. Strassburg: Heitz.
