Introduction
The early modern period saw the growing use of geometry as an instrument for solving structural problems in theoretical music, a change not independent from those that occurred in the conception of ratio in the context of theoretical music. In the early sixteenth century, the Bohemian mathematician and music theorist Erasmus of Höritz emerged as a German humanist who was very articulate in musical matters. In the context of the revival of interest in Greek sources, Erasmus communicated to musical readers an important product of such a revival and was likely the first in the Renaissance to explicitly apply Euclidean geometry to solve problems in theoretical music. Although Erasmus also considered the tradition of De institutione musica by Boethius, he based his ideas strongly on Euclid’s The Elements, using geometry in his own De musica in different ways in order to solve musical problems. It is this comprehensive geometrical work rather than the arithmetical and musical books of Boethius that served as Erasmus’ starting point. However, Erasmus proposed a proportional numerical division of the whole tone interval sounding between strings with a length ratio of
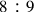 , since it was a primary arithmetical problem. This chapter aims at showing the implications of such a procedure of Erasmus for the transformation of the conception of ratio and for the emergence of the idea of real numbers in theoretical music contexts.
, since it was a primary arithmetical problem. This chapter aims at showing the implications of such a procedure of Erasmus for the transformation of the conception of ratio and for the emergence of the idea of real numbers in theoretical music contexts.
In order to do that, a passage will be considered here from chapter 17 of Book VI of Erasmus De musica, entitled Propositio decimaseptima Toni proportionem scilicet sesquioctavam in duas proportiones equales artificialiter et geometrice dividere.1 It concerns the equal and proportional numerical division of the whole tone interval sounding between strings with a length ratio of
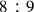 , a problem which confused the musical theorists from antiquity up to the Renaissance, and that played an important part in the historical process leading to the emergence of equal temperament. In this passage, Erasmus seemed to be in a position to solve such a problem.
, a problem which confused the musical theorists from antiquity up to the Renaissance, and that played an important part in the historical process leading to the emergence of equal temperament. In this passage, Erasmus seemed to be in a position to solve such a problem.
Division of the Tone
The problem of the division of the tone arose from the Pythagorean discovery of numerical indivisibility of a superparticular or epimoric ratio, i.e.,
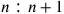 , by its geometrical mean, in particular applicable to the division of the ratio
, by its geometrical mean, in particular applicable to the division of the ratio
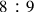 . Given
. Given
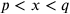 , where
, where
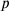 and
and
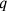 are integers and the ratio
are integers and the ratio
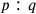 is superparticular,
is superparticular,
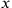 cannot be both an integer and at the same time fulfill the condition
cannot be both an integer and at the same time fulfill the condition
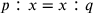 ; that is, it cannot be the geometric mean of
; that is, it cannot be the geometric mean of
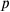 and
and
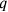 . Mathematically, the equal division of the tone
. Mathematically, the equal division of the tone
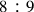 provides ratios involving surds or incommensurable ratios underlying musical intervals. These procedures were considered impossible by Pythagoreans in theoretical music, since these intervals could be determined only by ratios of integer numbers.
provides ratios involving surds or incommensurable ratios underlying musical intervals. These procedures were considered impossible by Pythagoreans in theoretical music, since these intervals could be determined only by ratios of integer numbers.
Attempts to divide the tone had, however, already been done since antiquity by Aristoxenus (fourth century BCE), who conceived of the theoretical nature of music as essentially geometric, understanding pitches, musical intervals, and also distances as continuous quantities that should follow the rules of Euclidean geometry and should be capable of being divided continuously. This inevitably raises questions concerning the nature of ratio in this context. Traditionally it is considered that Aristoxenian music theory rejected the position of the Pythagoreans in the sense that musical intervals should properly be expressed only as mathematical ratios involving whole numbers, and asserting instead that the ear was the sole guide for musical phenomena (Winnington-Ingram 1995, 592). It did not mean however that Aristoxenus’ theory could not be put on the same mathematical basis related to the developments in Greek mathematics of his time. Aristoxenus preferred geometry to arithmetic to solve problems involving relations between musical pitches and believed in the possibility of dividing the tone into two equal parts, conceiving of musical intervals and ratios as continuous magnitudes.
Such an idea unleashed many reactions, expressed, for instance, in the Sectio Canonis (Barbera 1991, 125) and much later in Boethius’ De institutione musica (Bower and Palisca 1989, 88), which stood in a strong Pythagorean tradition in theoretical music in the Middle Ages. Following the Pythagorean tradition, many medieval musical theorists maintained the impossibility of the equal division of the tone, which would mathematically lead to incommensurable ratios underlying musical intervals. Such a position began to change in the fifteenth century and was eventually systematically overcome in the early Renaissance through scholars like Nicholas of Cusa, Erasmus of Höritz, Faber Stapulensis, Henricus Grammateus, Pedro Ciruelo, Juan Bermudo, and others, who proposed the equal division of tone mostly by means of geometry. In his Musica, Erasmus of Höritz made use of an abstract numerical procedure to propose a solution for the problem of the equal division of the tone, expressing, rather, as a number the geometrical mean between the terms of the ratio
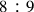 underlying the tone.
underlying the tone.
The De musica speculativa from Erasmus Horicius
Erasmus’ De musica emerged in a time when the rediscovery, translation, and publication of sources from antiquity, such as the works of Euclid, Archimedes, and Ptolemy, increased interest in and furthered the development of number theory. Gaps in the Pythagorean numerical system were quite disturbing, resulting in crisis and conceptual changes in the demarcation of the disciplines of arithmetic and geometry. So ratios involving surds, that is, incommensurable quantities, could only be discussed in the domain of continuous quantities and would demand the unification of two such disciplines as well as the conquest of a number continuum for mathematical activity.
Particularly for Erasmus, Arabic and Hindu concepts were highly influential since they promoted the development of Greek mathematics and handled entities such as negative and irrational numbers, and, with the introduction of Hindu numerals by Fibonacci, enabled computation of unprecedented complexity and the development of extremely large numbers. The latter was an important component in Erasmus’ division of the whole tone ratio, as will be seen in the following.
In chapter 17 of Book VI, Erasmus refers specifically to the division of the
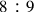 ratio, which represents the musical interval of a whole tone. In the four previous chapters of Book VI, Erasmus demonstrated incompletely the divisibility of other superparticular ratios into equal and proportional halves, like the octave
ratio, which represents the musical interval of a whole tone. In the four previous chapters of Book VI, Erasmus demonstrated incompletely the divisibility of other superparticular ratios into equal and proportional halves, like the octave
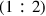 , fourth
, fourth
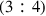 , fifth
, fifth
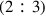 , and minor third
, and minor third
 .
.
In chapter 17, Erasmus proposed an abstract numerical procedure to find the geometrical mean between the terms of ratio
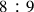 underlying the tone, expressing it as a number. He did not use the geometrical construction of mean proportional to two given straight lines from Proposition 13 of Book VI of Euclid, as did, for instance, Jacques Lefèvre d’Etaples in 1496, using exclusively non-numerical Euclidian methods capable of being carried out with a straightedge and compass.
underlying the tone, expressing it as a number. He did not use the geometrical construction of mean proportional to two given straight lines from Proposition 13 of Book VI of Euclid, as did, for instance, Jacques Lefèvre d’Etaples in 1496, using exclusively non-numerical Euclidian methods capable of being carried out with a straightedge and compass.
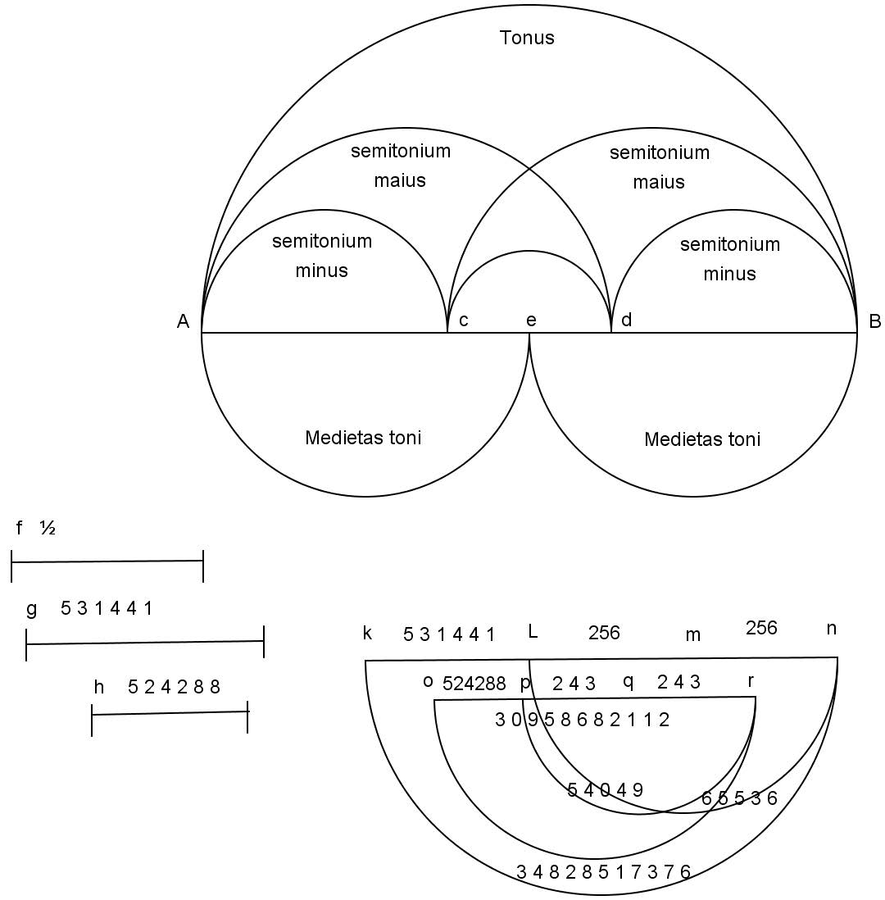
Fig. 16.1: Erasmus's arithmetical division of the tone, chapter 17, Book VI, De musica.
He attempted rather to reach an expression for the ratio for the supposedly equally proportional halves of the whole tone interval using very large integer numbers. He did it first using Proposition 15 of Book V of the Elements, which asserts that
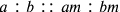 . Following his method, the half of the
. Following his method, the half of the
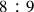 ratio of a tone could be obtained by the geometric mean of its expansion into the term
ratio of a tone could be obtained by the geometric mean of its expansion into the term
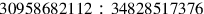 . This ratio was derived directly from
. This ratio was derived directly from
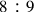 by multiplying numerator and denominator by the factor 3869835264, a procedure guaranteed by Proposition 15 of Book V for
by multiplying numerator and denominator by the factor 3869835264, a procedure guaranteed by Proposition 15 of Book V for
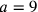 ,
,
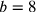 , and
, and
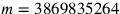 . The proportionality between the original ratio
. The proportionality between the original ratio
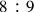 and
and
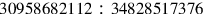 allows a mapping between intermediate terms of the ratio
allows a mapping between intermediate terms of the ratio
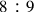 , including the mean. Numbers between the terms of its expansion are mapped into a large number ratio, considering that the interval determined by the expansion becomes subdivisible and that the greater the distance between the terms in the large number ratio, the greater the precision one can get for the intermediate terms of the ratio
, including the mean. Numbers between the terms of its expansion are mapped into a large number ratio, considering that the interval determined by the expansion becomes subdivisible and that the greater the distance between the terms in the large number ratio, the greater the precision one can get for the intermediate terms of the ratio
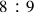 , represented by the large number between the two terms of the large number ratio. Since there were no decimal fractions at this time, the proportionally extended ratio is used for the purpose of extracting the square root with a high degree of precision, in this case associated with large integer numbers rather than with places after the decimal point. The larger the distance between the terms in the large number ratio, the higher the precision with which the geometrical mean is obtained. Nevertheless, Erasmus seemed not to worry about carrying out any computation in the text, and he did not present his result as an approximation of the true real number. He is the first author to propose an abstract numerical procedure for the given problem, expressing it as a number and avoiding using the construction of a geometrical line. Since it was an elementary arithmetical problem, it could be solved “artificialiter,” that is, numerically.
, represented by the large number between the two terms of the large number ratio. Since there were no decimal fractions at this time, the proportionally extended ratio is used for the purpose of extracting the square root with a high degree of precision, in this case associated with large integer numbers rather than with places after the decimal point. The larger the distance between the terms in the large number ratio, the higher the precision with which the geometrical mean is obtained. Nevertheless, Erasmus seemed not to worry about carrying out any computation in the text, and he did not present his result as an approximation of the true real number. He is the first author to propose an abstract numerical procedure for the given problem, expressing it as a number and avoiding using the construction of a geometrical line. Since it was an elementary arithmetical problem, it could be solved “artificialiter,” that is, numerically.
Erasmus asserts that “[...] in musical demonstrations we are forced to use all kinds of ratios [...] since not all shapes of consonances and also dissonances are founded in rational ratios and for that reason we must not neglect the ratios of surds” (Horitius ca. 1500, fo. 61v). Erasmus considered here incommensurable ratios or irrational numbers in musical contexts. At first sight, in order to make use of Eudoxus’ theory of Book V of Euclid’s Elements on which the theory of ratios of surds is based and wherein abstract quantities with continuous nature are dealt with, Erasmus established a link between continuous and discrete quantities.
It is possible to identify similar ideas concerning the relation between the numerical division of the tone proposed by Erasmus and Eudoxus’ Definition V of Book 5 of the Elements. Whereas Erasmus confined a searched irrational number by using only integers, Eudoxus’ definition corresponded, arithmetically speaking, to establishing a proportionality of ratios through the confinement of ratios with integer terms. In these analogous procedures, Erasmus and Eudoxus found precision in finding an irrational number and in establishing a proportionality between two given ratios, respectively, through ratios with big terms. Erasmus made use of The Elements; nevertheless, his source was the Campanus’ translation, which had an arithmetical terminology not derived from the geometrical ratio theory of Book V of Euclid, but instead from a number of different sources, very likely including Arithmetic by Jordanus de Nemore from the thirteenth century. On the one hand, such a fact makes it implausible that Erasmus had access to Eudoxus’ definition in the original sense and, on the other hand, makes the strong and curious structural analogy between both procedures very compelling.
Erasmus realized that the search for a geometrical mean to the ratio underlying the whole tone could not result in a rational number, and instead of changing the domain at this point from a discrete quantity of numbers to a continuous quantity of geometrical lines, he established a link between continuous and discrete quantities, proposing a number continuum, although not explicitly, thus creating a very dense discrete point set in the space between the original terms 8 and 9 by their expansion.
Concluding Remarks
It is conceivable that if Erasmus really thought he could divide the sesquioctave ratio in terms of a purely numerical operation, he must have possessed an at least rudimentary concept of the number continuum. Such an assumption is corroborated by a passage appearing later on in chapter 17, where he seems to refer directly to the idea of such a continuum, mentioning Boethius as a prisoner of the Pythagorean doctrine of discrete integer numbers, not accessing all ratios of numbers (Horitius ca. 1500, fo. 67v). Just before this passage, Erasmus asserts that exactly half of the whole tone interval would be provided by extracting the square root of the product of its terms 8 and 9, which would be
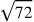 (Horitius ca. 1500, fo. 67v). He did not, however, relate this result explicitly to the computations he presented. He obtained the large number ratio, but the geometrical mean between the two terms still needed to be found. Since he presented the method of doing this by extracting the square root of
(Horitius ca. 1500, fo. 67v). He did not, however, relate this result explicitly to the computations he presented. He obtained the large number ratio, but the geometrical mean between the two terms still needed to be found. Since he presented the method of doing this by extracting the square root of
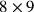 , one might ask why he did not do it from the ratio
, one might ask why he did not do it from the ratio
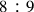 , or if he produced the proportionally large number ratio, how could he use this representation to the extraction mentioned above and to approach the geometrical mean. It might be assumed that he left it to the reader.
, or if he produced the proportionally large number ratio, how could he use this representation to the extraction mentioned above and to approach the geometrical mean. It might be assumed that he left it to the reader.
Theoretically based on many geometrical propositions and, unusually, based on the Euclidean style, Musica deals with ratio as a continuous quantity, announcing perhaps what would emerge as an arithmetical treatment of ratios in theoretical music contexts during the sixteenth century, approaching ratio to a real number. Interestingly, Erasmus could have easily solved the equal division of the tone by making use of the proposition of Euclid’s Elements that provides the geometrical mean as the height of a right-angled triangle. Nevertheless, missing the concept of infinity, he preferred to use a numerical method to approach such a mean, although his procedure was not recognizable as an approximation of the true real number value of the geometrical mean. Erasmus provided a mathematical theoretical structure for a virtual pitch relation space, a continuum of rational numbers that can be seen as an important step for laying the foundations for the real number system.
References
Barbera, André (1991). The Euclidean Division of the Canon. Lincoln: University of Nebraska Press.
Bower, Calvin M. and Claude V. Palisca, eds. (1989). Fundamentals of Music: Anicius Manlius Severinus Boethius. New Haven, London: Yale University Press.
Horitius, Erasmus (ca. 1500). De Musica. Reg. Lat. 1245, Biblioteca Apostolica Vaticana.
Palisca, Claude V. (1994). The Musica of Erasmus of Höritz. In: Studies in the History of Italian Music and Music Theory. Oxford: Clarendon Press, 146–67.
Winnington-Ingram, Reginald Pepys (1995). Aristoxenus. In: The New Grove Dictionary of Music and Musicians. Vol. 1. Ed. by Stanley Sadie. London: Macmillan, 592.

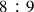 ) of the Whole Tone into Two Equal Ratios, Artificially and Geometrically.
) of the Whole Tone into Two Equal Ratios, Artificially and Geometrically.