La strumentazione scientifica è un aspetto poco conosciuto, e tuttavia di notevole importanza, dell’opera di Guidobaldo del Monte. Nella ricognizione del materiale manoscritto e a stampa dello scienziato pesarese, abbiamo cercato di mettere ordine, anche cronologicamente, nelle numerose testimonianze relative all’invenzione, perfezionamento, utilizzo di numerosi apparati e dispositivi meccanici, destinati sia a impieghi di ordine pratico, sia a scopi osservativi e sperimentali.
In questo spiccato interesse verso gli strumenti scientifici un ruolo di primaria importanza assunse, nell’ambito del vivace e stimolante ambiente scientifico del ducato, la nascita e lo sviluppo a Urbino verso la metà del Cinquecento di una officina specializzata nella costruzione di strumenti scientifici che presto ottenne vasta fama. Fondatore dell’officina e capostipite di una lunga ed importante schiera di artigiani-meccanici urbinati fu Simone Barocci
È noto che un’importante porzione dell’opera di Guidobaldo sia stata spesa, sul piano teorico, nel tentativo di sistematizzare la teoria delle macchine semplici; in tale sforzo assiomatico-dimostrativo egli non perse mai di vista la necessità di evidenziare una concordanza teoria-pratica, mettendo in luce la componente empirico-operativa e rimarcando l’utilità pratica delle “discipline mathematiche.” Sotto questo punto di vista la presenza di una qualificata officina di meccanici nel ducato dovette rappresentare per il nostro un forte stimolo non solo verso una più meditata concettualizzazione della meccanica, ma anche per studiare ed approfondire le applicazioni pratiche delle discipline matematiche che allora avevano, quali discipline “subalternate,” la topografia, la “scientia” delle macchine, la prospettiva, l’architettura civile e militare, la cartografia.
In aggiunta Guidobaldo ebbe l’opportunità di vivere in un contesto culturale di altissimo livello per la presenza nel ducato di figure quali Federico Commandino (1509–1575)
Poteva inoltre beneficiare di quella tradizione architettonica iniziata ai tempi di Federico da Montefeltro
È probabile che l’elenco degli strumenti che qui presentiamo, individuati tra gli scritti, o semplicemente grazie a testimonianze coeve e successive, non sia esaustivo di tutta la produzione scientifica di Guidobaldo; non si dimentichi che molte sue carte ed opere andarono perdute e che non sempre l’ideazione e la realizzazione di strumenti scientifici veniva accompagnata da registrazioni scritte. C’è un’importante testimonianza del figlio di Guidobaldo, Orazio, il quale scrivendo a Galileo
10.1 Gli strumenti di Guidobaldo
Al fine di facilitare la distinzione tra funzioni e contesti d’uso, abbiamo ritenuto utile fornire una classificazione di massima degli strumenti scientifici elaborati da Guidobaldo inserendo in essa sia quelli da lui ideati, sia quelli perfezionati. Nello schema è stato assegnato ad ogni strumento una data che primariamente vuole indicare l’anno d’invenzione; quando ciò non è stato possibile si è riportata la data della prima realizzazione nota.
Strumenti da disegno: ellissografo (1579), strumento a regoli e a filo per l’iperbole (1587 c.), compasso per circonferenze a largo raggio (1579)
Strumenti per il rilevamento: teodolite astronomico (1579c.), squadro (1589c.)
Strumenti di calcolo: compasso di proporzione (1570c.), moltiplicatore meccanico delle frazioni di grado (1579)
Strumenti come apparati sperimentali: libra (1577), sistemi di carrucole (1577), bilancia idrostatica (1587c.)
Strumenti per la misura del tempo: orologio solare a rifrazione tipo calice (1572), orologio solare a rifrazione tipo fontana (1587–1601).
Naturalmente ogni classificazione ha sempre qualcosa di arbitrario e la nostra non sfugge a tale regola. Ad esempio il compasso di proporzione può essere inteso, ad un tempo, come strumento da disegno oltre che di calcolo, perché risolve il problema di dividere un segmento, o una circonferenza, in un numero prefissato di parti uguali.
Infine va segnalata l’assenza di strumenti di tipo prospettico, nonostante che Guidobaldo pubblichi il più importante testo di prospettiva5 del XVI secolo, nel quale non compare nessuno strumento. Analizziamo ora ciascuno dei punti della classificazione.
10.2 Strumenti da disegno
Nel 1579 Guidobaldo pubblica a Pesaro un’opera di notevole spessore scientifico, il Planisphaeriorum universalium theorica (Monte 1579), diviso in due libri, dove affronta il problema, allora assai dibattuto, della risoluzione della sfera celeste sul piano. La questione aveva assunto operativamente una notevole importanza con la diffusione in Occidente dell’astrolabio da parte degli arabi. L’utilizzo della proiezione stereografica polare aveva costretto i vari costruttori a dotare gli astrolabi di un numero sempre maggiore di dischi ciascuno dei quali forniva la rappresentazione della sfera celeste per una data latitudine. Questa proiezione, utilizzata operativamente all’inizio del Cinquecento da Johannes Stöffler
10.2.1 Il compasso per circonferenze ad ampio raggio
Nel primo libro del Planisphaeriorum Guidobaldo dimostra per la prima volta che gli elementi proiettivi del planisfero di Gemma Frisio
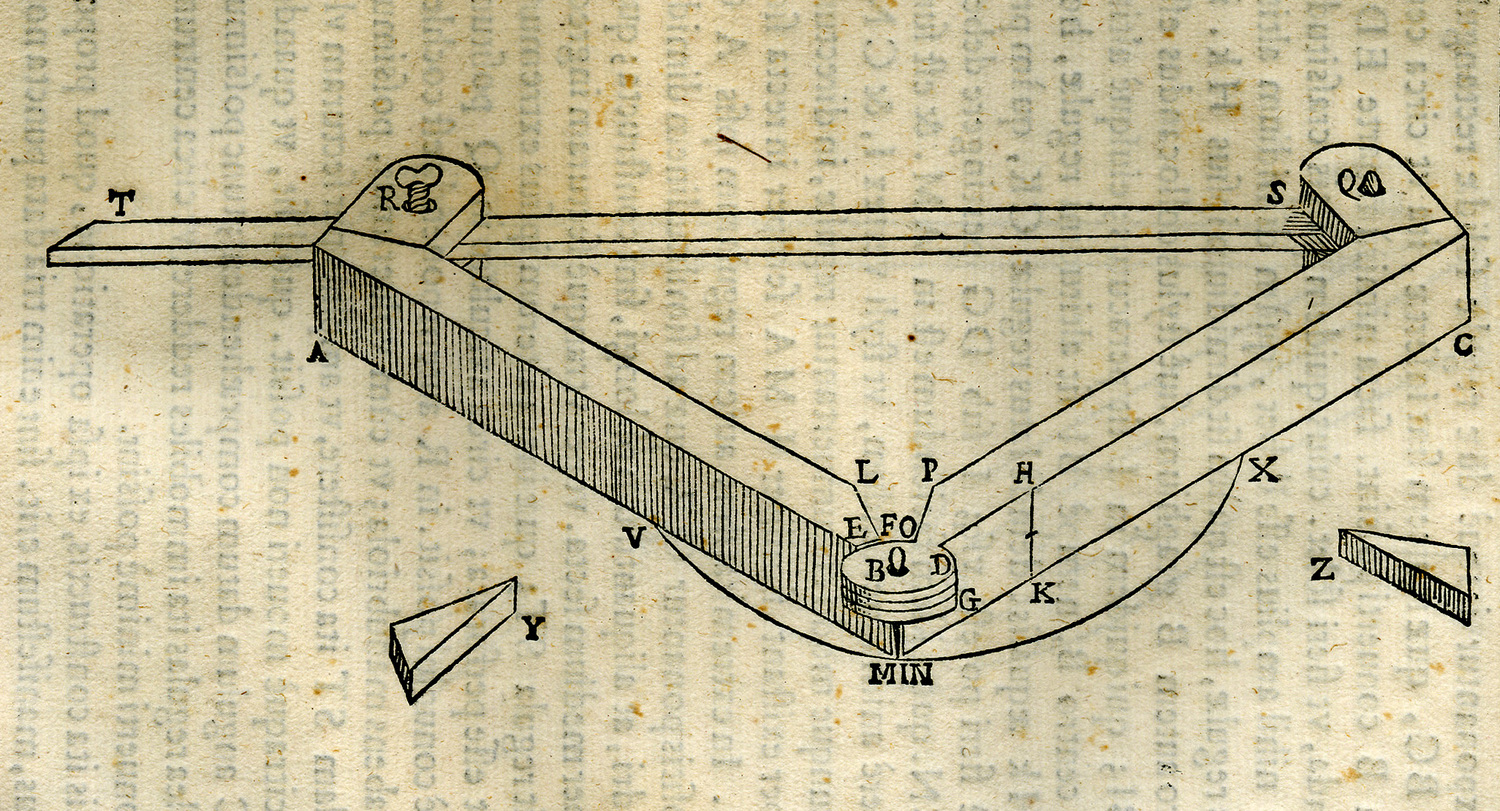
fig. 10.1: Compasso per circonferenze a largo raggio. Planisphaeriorum universalium theorica, Pesaro 1579. Bibl. Oliveriana, Pesaro.
10.2.2 L’ellissografo
Nel secondo libro del Planisphaeriorum Guidobaldo dimostra per la prima volta che nella proiezione ortografica equinoziale del planisfero di de Rojas
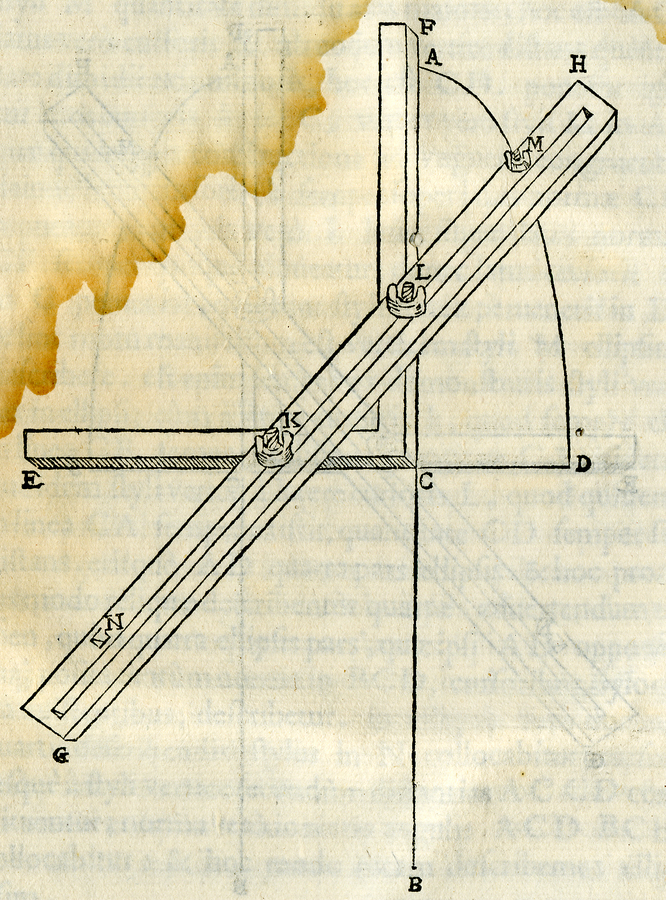
fig. 10.2: L’ellissografo. Planisphaeriorum universalium theorica, Pesaro 1579. Bibl. Oliveriana, Pesaro.
Lo strumento è costituito da una squadra e da un regolo in cui è praticata una scanalatura nella quale possono scorrere ed essere bloccati in qualsiasi posizione due cursori. Uno stilo può essere fissato a piacere in uno dei due fori11 agli estremi del regolo a seconda che si voglia disegnare il quarto di ellisse superiore o inferiore. Inizialmente si regola la distanza tra i cursori in modo che siano spaziati secondo la differenza tra i due semiassi. Posizionata la squadra lungo i semiassi dell’ellisse è sufficiente far scorrere i cursori lungo i lati della squadra per tracciare il quarto d’ellisse. Un primo aspetto notevole da sottolineare consiste nel modo con cui Guidobaldo presenta l’ellissografo, fornendo le immagini dello strumento completo, di alcune delle parti che lo compongono, e degli esplosi (Monte 1579, 105–106; Figure 10.3 e 10.4) fatto più unico che raro per un testo del 1579.
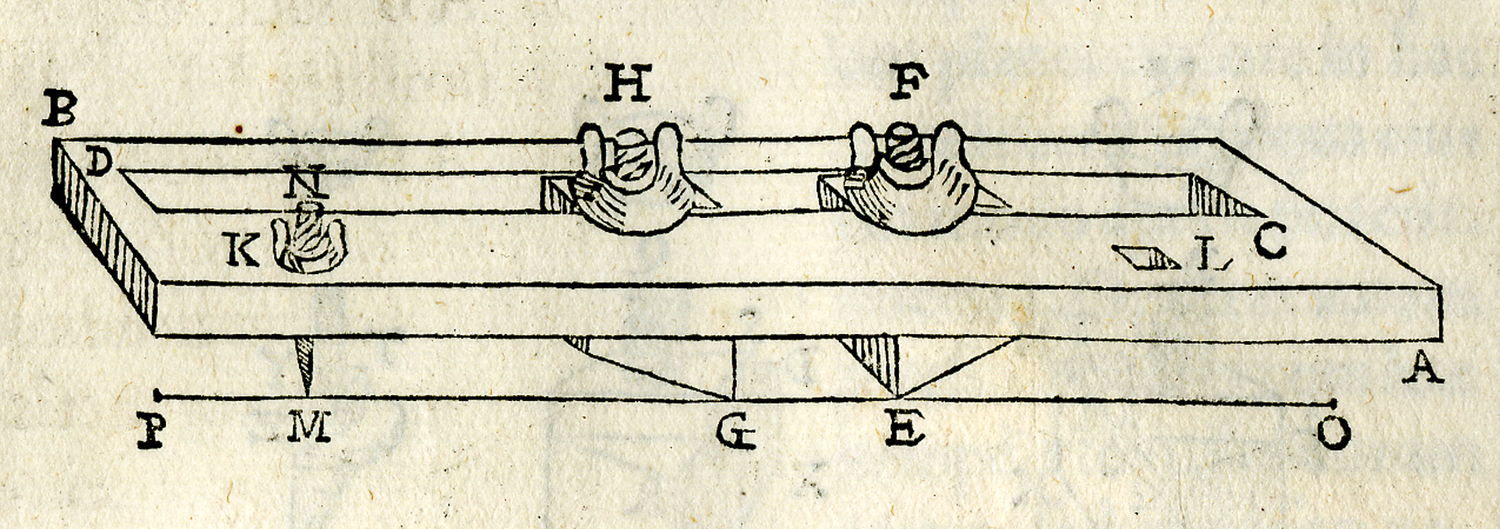
fig. 10.3: Particolare dell’ellissografo. Bibl. Oliveriana, Pesaro.
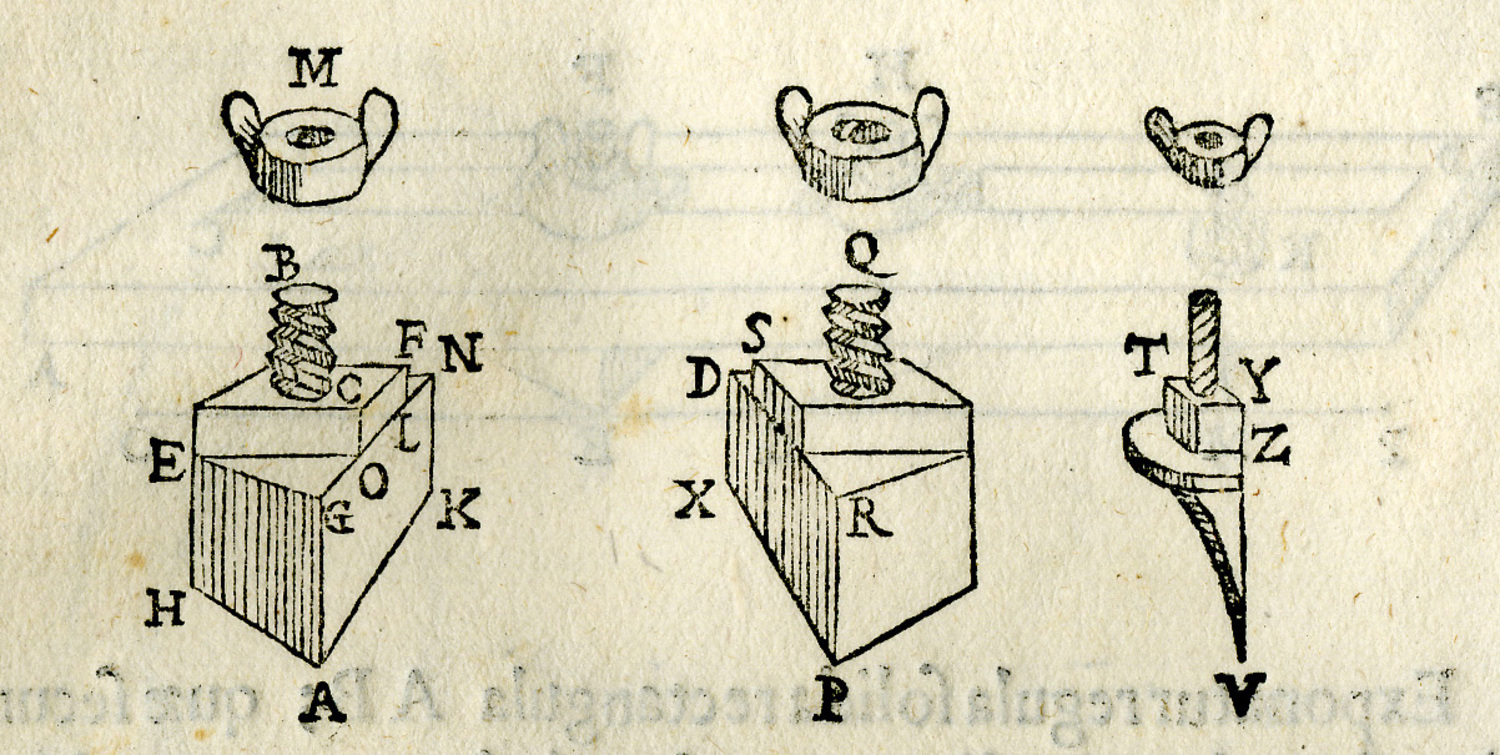
fig. 10.4: Particolare dell’ellissografo, in esploso. Bibl. Oliveriana, Pesaro.
Insomma Guidobaldo si prende cura di fornire dettagliate informazioni per la costruzione in officina dello strumento (ricordando molto probabilmente le domande in proposito dell’artefice Simone Barocci
La seconda considerazione riguarda la sua diciamo “derivazione” dallo strumento di Nicomede13
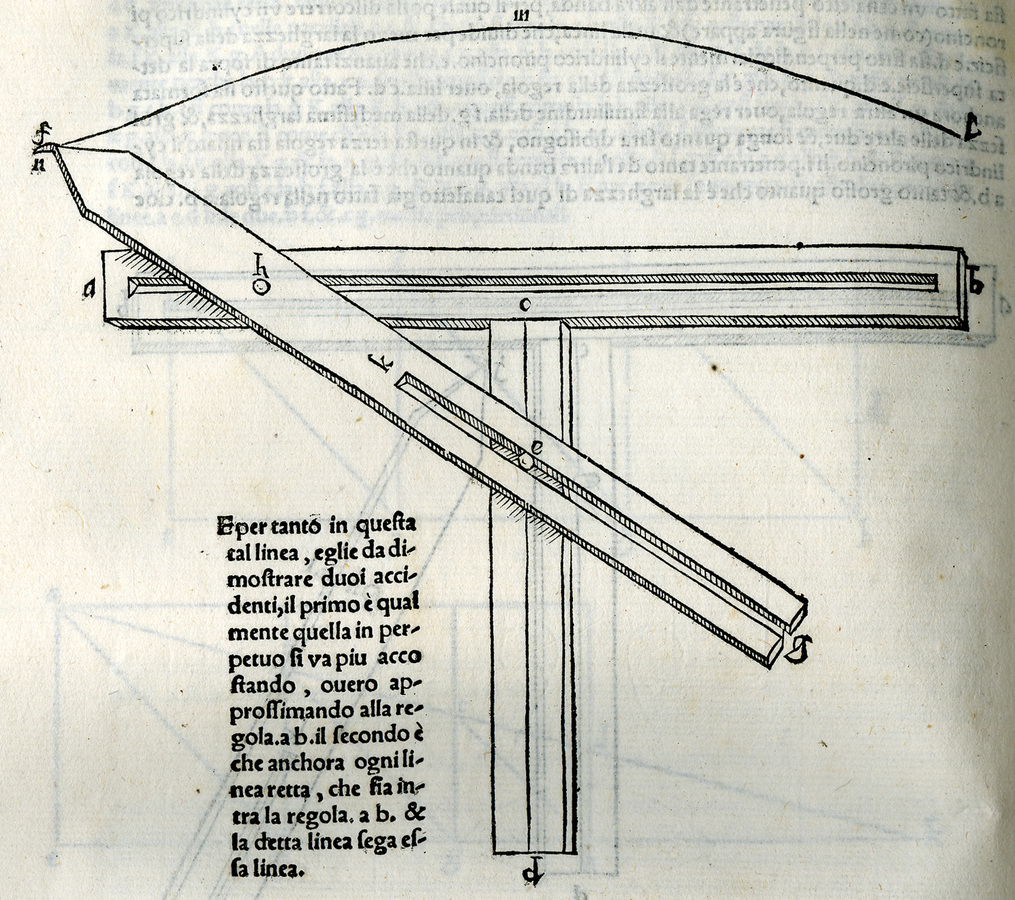
fig. 10.5: Strumento di Nicomede per tracciare la concoide. General trattato de numeri et misure, parte quinta, Venezia 1560. Bibl. Oliveriana, Pesaro.
È evidente che analiticamente la concoide ha ben poco a che fare con l’ellisse, ma per configurazione meccanica i due strumenti sono molto simili. Basta infatti rendere mobile il punto fisso e perché lo strumento di Nicomede tracci ellissi anziché concoidi. Ciò è interessante perché fa comprendere come venivano sviluppati gli strumenti polivalenti. Ad esempio, l’urbinate Felice Paciotti
10.2.3 Strumento per disegnare l’iperbole
Nel manoscritto parigino delle Meditatiunculae15 compare uno strumento per tracciare le iperboli, presentato in due versioni, a regoli e a filo (Figure 10.6 e 10.7).16
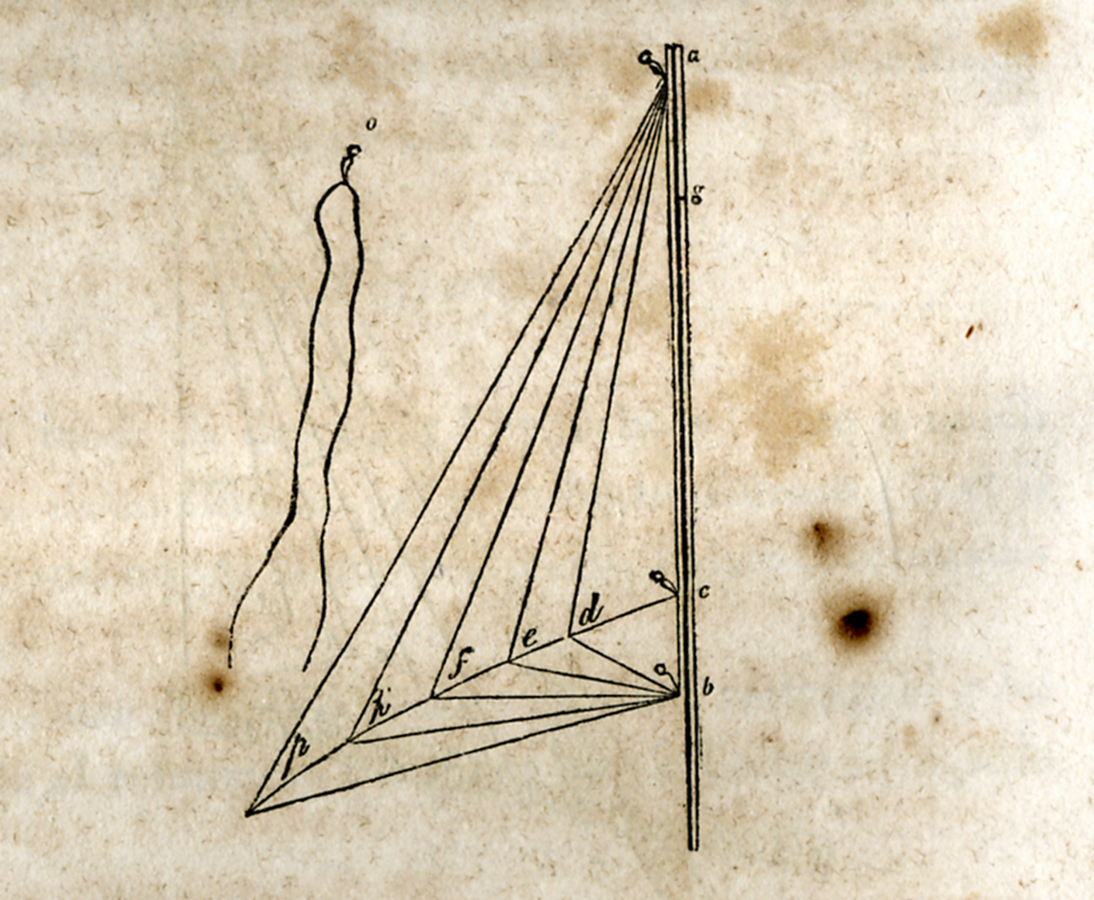
fig. 10.6: Strumento a fili per disegnare l’iperbole. Da Meditatiunculae, Bibliothèque Nationale, Parigi.
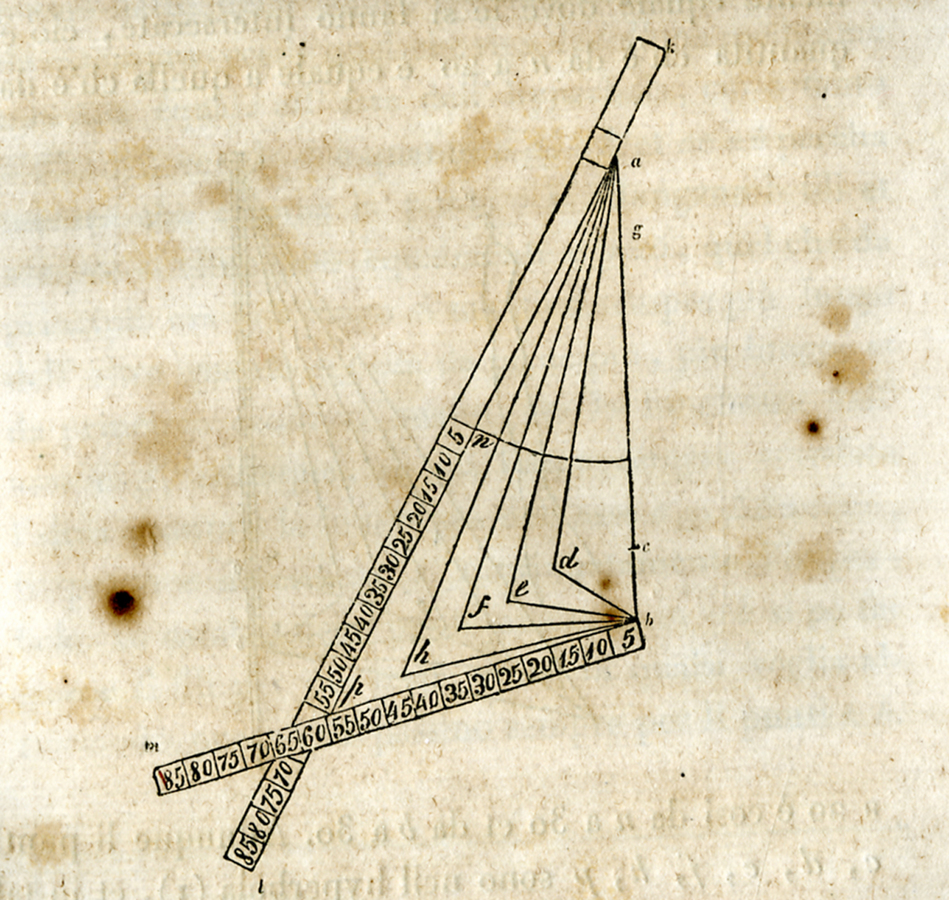
fig. 10.7: Strumento a regoli per disegnare l’iperbole. Da Meditatiunculae, Bibliothèque Nationale, Parigi.
A questo proposito Guidobaldo cita un passo del Liber de horologiorum dove il Commandino
10.3 Strumenti per il rilevamento
10.3.1 Lo squadro
Guidobaldo era anche un tecnico di prim’ordine: soprintendeva alla costruzione e riparazioni di acquedotti, ispezionava le fortificazioni, faceva prove di tiro con l’artiglieria, studiava come rendere più efficienti le macchine, era naturale che prestasse la sua attenzione anche all’agrimensura. Nelle pagine iniziali delle Meditatiunculae troviamo un capitoletto intitolato Del misurar18 nel quale Guidobaldo descrive preliminarmente i metodi geometrici di Leon Battista Alberti e Gemma Frisio
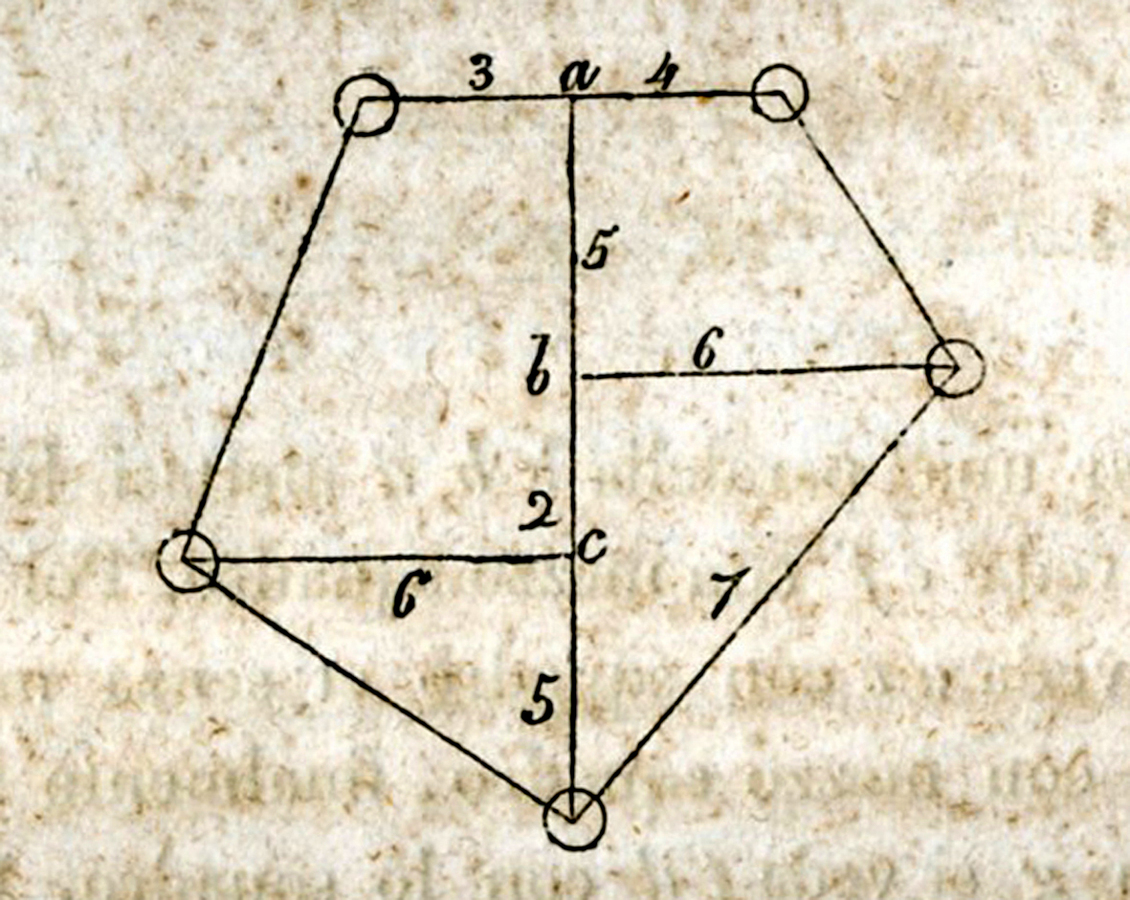
fig. 10.8: Uso dello squadro agrimensorio. Da Meditatiunculae, Bibliothèque Nationale, Parigi.
Il metodo utilizzato è quello di scomporre le superfici in triangoli e trapezi rettangoli utilizzando uno o più punti di stazione. Lo strumento nella versione di Guidobaldo è costituito da un cilindro avente fenditure “spaccature” longitudinali20 a 90° e a 45° che forniscono i seguenti angoli fissi di traguardo: 45°, 90°, 135°, 180°, 225°, 270°. La forma cilindrica dello squadro, a differenza del modello a disco piatto21, presentava notevoli vantaggi in quanto forniva piani anziché linee visuali, permettendo di traguardare angoli anche su terreni non pianeggianti.22 Un’altra notevole caratteristica tecnica dell’apparato è lo snodo mediante il quale lo squadro è connesso al sostegno; con esso era possibile disporre orizzontalmente il piano della fenditura principale così da avere a disposizione, tramite le altre fenditure, un angolo visuale di 45° per misurare le altezze. Guidobaldo presenta lo squadro nella forma cilindrica che si manterrà tale per secoli. Ad esso l’architetto urbinate Muzio Oddi
10.3.2 Il teodolite astronomico
All’inizio dei Problematum astronomicorum libri septem, pubblicati postumi a Venezia nel 1609 (Monte 1609, ff. 2v–3v), Guidobaldo, dopo aver affrontato il problema delle scale graduate, propone uno strumento (Monte 1609, ff. 7r–7v) per rilevare l’altezza e l’azimut dei corpi celesti, cioè una sorta di teodolite astronomico (Figura 10.9).
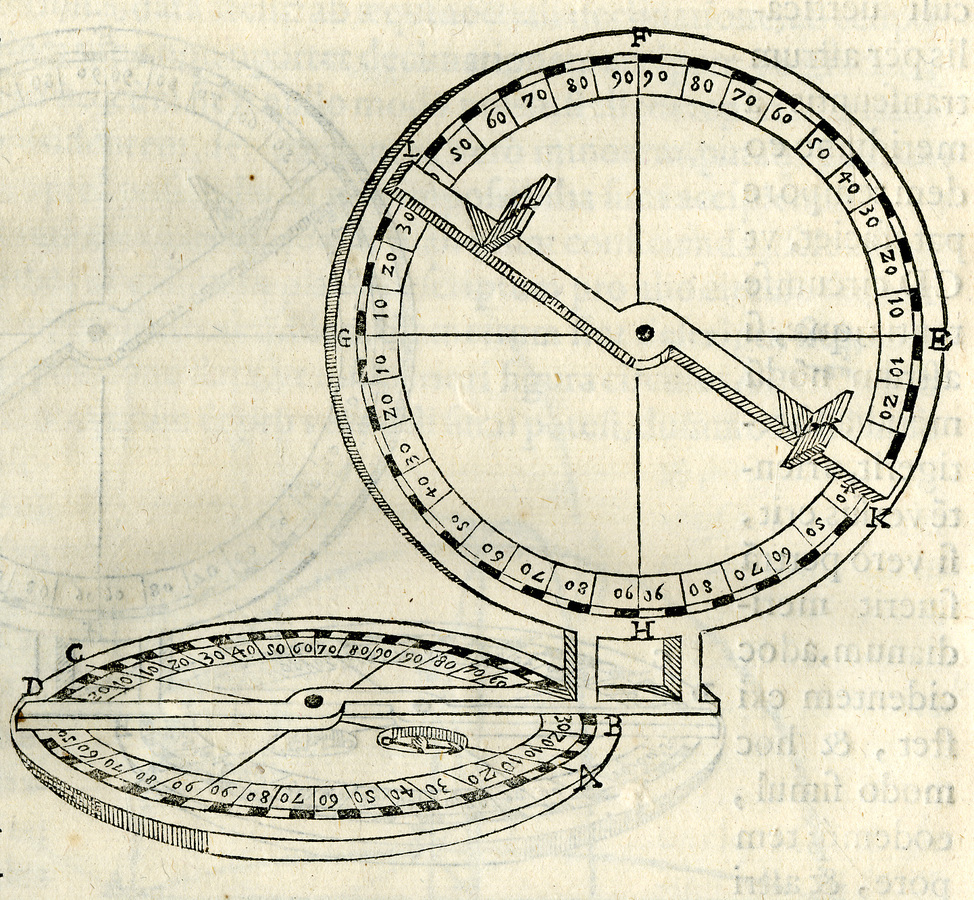
fig. 10.9: Il teodolite astronomico di Guidobaldo. Problematum astronomicorum libri septem, Venezia 1609. Bibl. Oliveriana, Pesaro.
La sua conformazione è molto simile a quella del teodolite terrestre le cui origini vengono generalmente ricondotte al modello24 di Leonard Digges

fig. 10.10: Il teodolite di Cosimo Bartoli. Del modo di misurar
Si noti però che il teodolite del Bartoli
D’altra parte la Mechanica di Tico Brahe26 era ben nota nell’ambiente urbinate e sarebbe quindi poco probabile supporre che Guidobaldo l’avesse di proposito ignorata, più plausibilmente, pur cogliendo l’importanza della precisione osservativa,27 non si rendeva conto che la strumentazione astronomica andava di fatto rivoluzionata e che il metodo da lui proposto di rilevazione delle frazioni di grado non poteva essere in alcun modo un’alternativa “povera” alla costosissima strumentazione ticonica. Occorre tuttavia aggiungere che la comunità scientifica urbinate dedicava poca attenzione all’astronomia in generale e meno ancora verso quella osservativa.28 Nei Problematum, così come nel Planisphaeriorum, Guidobaldo si rivela un ottimo conoscitore delle tecniche matematiche che cerca di rendere più agevoli procedendo per via geometrica, ma non mostra altrettanto interesse e competenza per gli aspetti osservativi e operativi della raccolta-dati. In definitiva Guidobaldo non coglie l’importanza fondamentale del programma proposto da Brahe
10.4 Strumenti di calcolo
10.4.1 Il compasso a due scale
Muzio Oddi
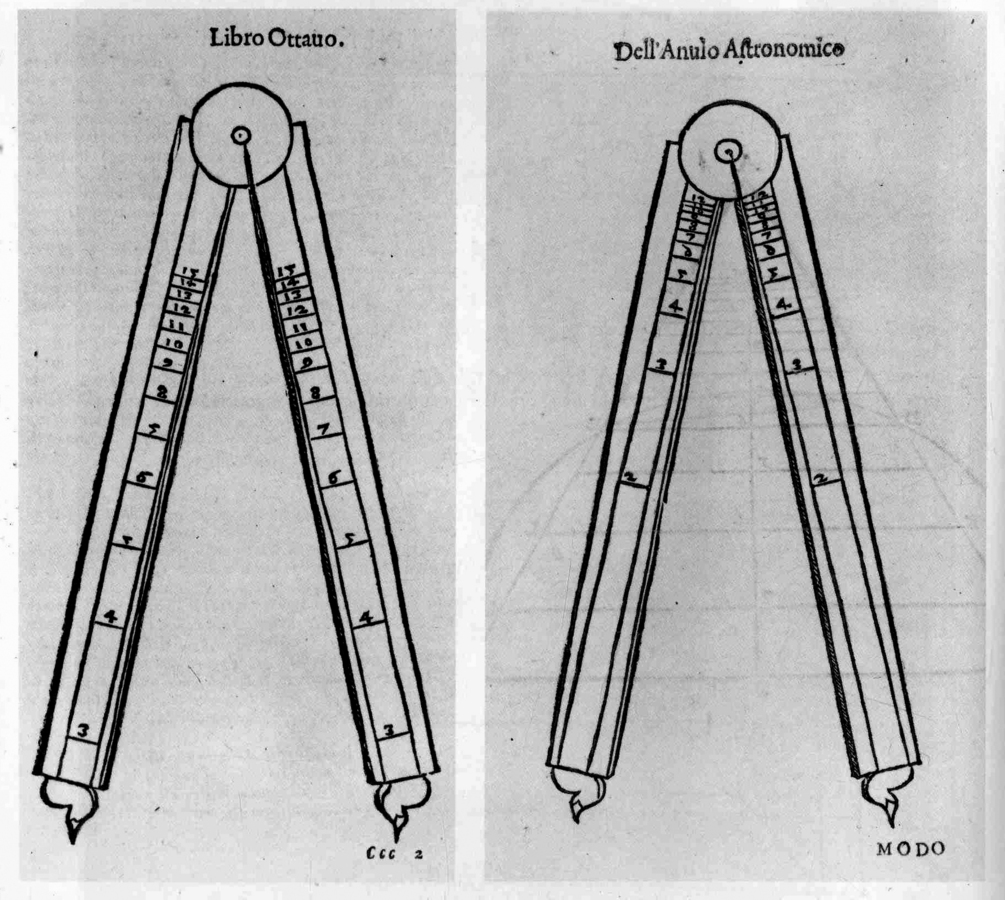
fig. 10.11: Il compasso di Guidobaldo. Giovanni Paolo Gallucci, Della fabrica et uso di diversi stromenti di astronomia et cosmografia, Venezia 1598.
Inoltre i due regoli si prestano a ospitare altre scale per altri usi, e questo avvalora la rielaborazione di Guidobaldo perché ha consentito ulteriori sviluppi dello strumento.29
10.4.2 Il moltiplicatore meccanico delle frazioni di grado
Completamente diverso è lo strumento ideato da Guidobaldo per calcolare le frazioni di grado la cui descrizione si trova nei Problematum astronomicorum. Si tratta di un dispositivo meccanico che esegue automaticamente la moltiplicazione per 60 non solo delle frazioni di grado, ma anche dei primi, dei secondi, dei “terzi,” dei “quarti,” ecc. Il problema, spiega Guidobaldo, può essere preliminarmente affrontato e risolto per via geometrica mediante un normale compasso.30 Ad esempio se l’alidada traguarda un angolo compreso tra 26° e 27°, la procedura da utilizzare risulta semplice: con le punte del compasso si riprende sulla scala graduata la frazione di grado eccedente i 26°, quindi, partendo dal fondo scala, la si riporta sulla medesima scala per 60 volte. La divisione della scala su cui essa cade indicherà i primi; se non si ottiene l’esatto allineamento con una divisione, si riporta sempre col compasso la frazione di primo così ottenuta a fondo scala e si ripete la procedura prima esposta ottenendo i secondi, e così di seguito, con un processo iterativo, fino a intercettare esattamente una divisione. Guidobaldo esegue queste operazioni tutte su una medesima scala31 con graduazione da 0° a 60.° Il metodo, oltre al dispendio di tempo, pone il problema della precisione e dell’accuratezza delle misure iterate. Per ovviare ciò Guidobaldo, ispirandosi all’orologeria, propone un dispositivo meccanico rapido, e a suo parere preciso, che esegue automaticamente una moltiplicazione per 60.32 Si tratta di un sistema di quattro ingranaggi che fa corrispondere a una rotazione di un indice su un quadrante, 60 rotazioni di un altro indice su di un quadrante opposto. Di conseguenza alla rotazione di un arco di 1° corrisponde, sull’altro quadrante, la rotazione di 60° (Figure 10.12 e 10.13).
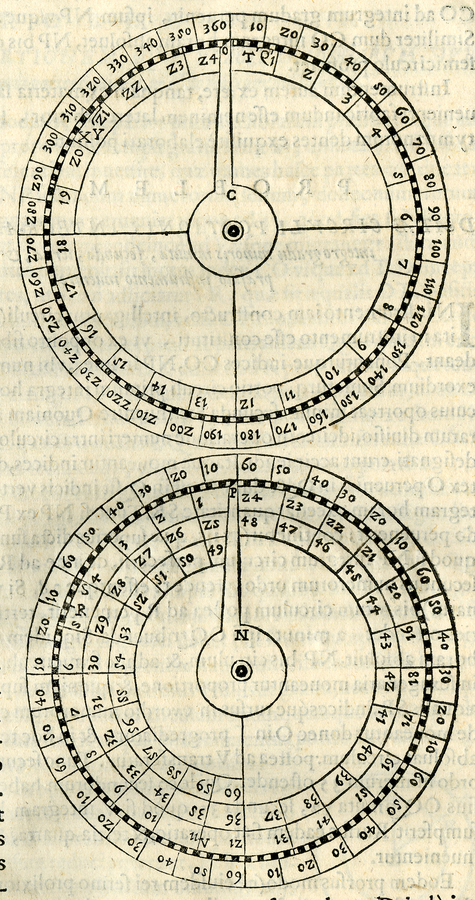
fig. 10.12: Quadranti e indici del calcolatore meccanico delle frazioni di grado. Problematum astronomicorum, Venezia 1609. Bibl. Oliveriana, Pesaro.
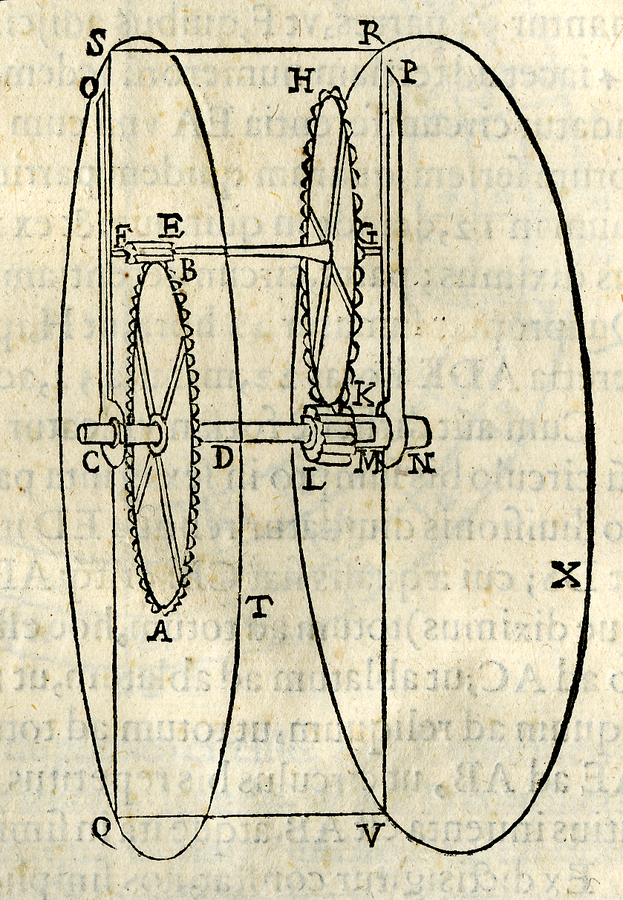
fig. 10.13: Il sistema di ingranaggi del calcolatore meccanico. Problematum astronomicorum, Venezia 1609. Bibl. Oliveriana, Pesaro.
Da una citazione sappiamo che lo strumento era in gestazione fin dal 1579.33 Va però precisato che l’idea dell’amplificazione meccanica delle frazioni di grado non è di Guidobaldo bensì del veneziano Giacomo Contarini
Nella storia dell’astronomia il sistema meccanico per la rilevazione delle frazioni di grado non avrà alcun seguito.35 L’idea, seppur suggestiva, era tecnicamente errata. Guidobaldo, come abbiamo precedentemente detto, non coglie il vento del progresso tecnico che stava rivoluzionando la strumentazione astronomica (in particolare con l’opera e la strumentazione del Brahe)
Resta infine il dubbio che la mancata pubblicazione da parte di Guidobaldo dei sette libri dei Problematum possa essere dovuta proprio a dei ripensamenti del nostro sull’opera del Brahe
10.5 Strumenti come apparati ‘sperimentali’
Sfogliando il Mechanicorum liber (Monte 1577) è inevitabile accorgersi di una marcata asimmetria dell’opera: i primi due capitoli, sulle leve e sulle carrucole, occupano infatti ben 208 pagine, mentre ai restanti tre capitoli sul verricello, cuneo e vite vengono dedicate solo 50 pagine.
A parte la fretta di dare alle stampe il volume, la ragione principale ci sembra prevalentemente di ordine metodologico. Nello studio delle proprietà di leve e carrucole Guidobaldo procede basandosi su prove empiriche realizzate mediante apparati che egli progetta appositamente per le sue ricerche. Sotto questo punto di vista i primi due libri del Mechanicorum godono di un’impalcatura empirico-strumentale che sembra mancare agli altri tre libri. Sarebbe forse esagerato parlare di fisica sperimentale, tuttavia si tratta di una “statica strumentale” che le è molto vicina.
10.5.1 La libra
Il primo apparato discusso nel Mechanicorum è la libra, ossia una leva a bracci uguali avente il baricentro coincidente con il centro di sospensione e alle cui estremità sono posti pesi uguali. Guidobaldo la studia a fondo per sostenere il proprio punto di vista su una polemica allora in atto e dimostrare così l’esistenza dell’equilibrio indifferente. La controversia oppone Guidobaldo, che difende l’equilibrio indifferente, al Cardano, Tartaglia
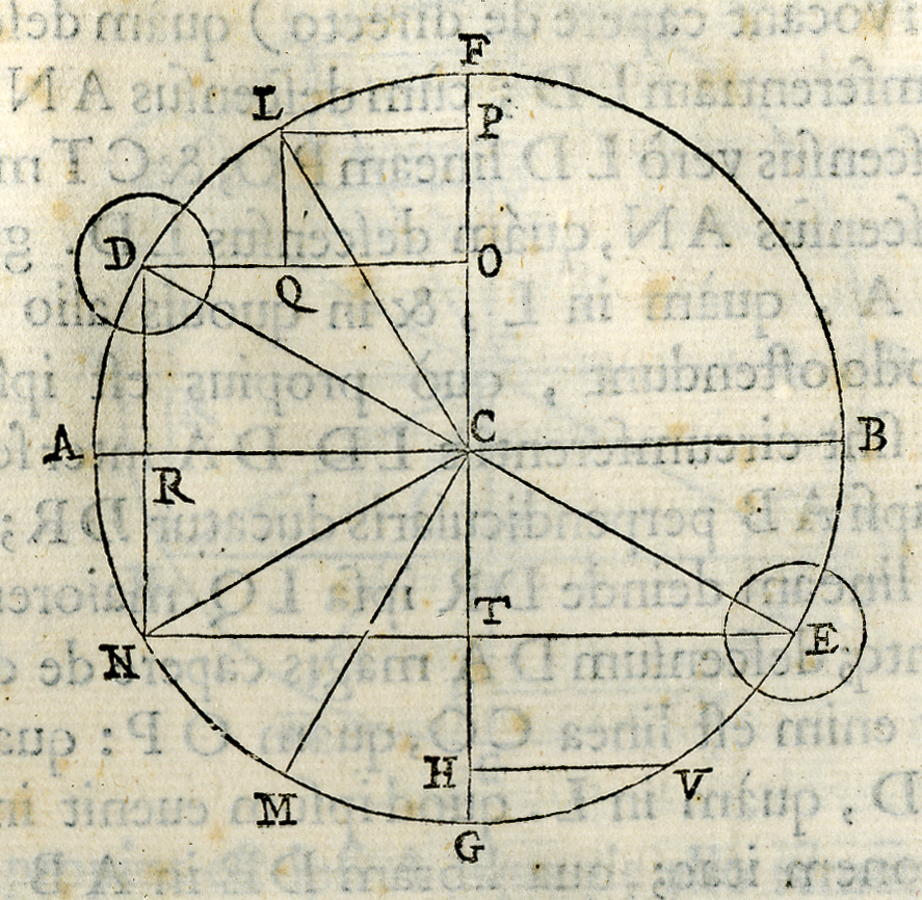
fig. 10.14: La libra. Mechanicorum liber, Pesaro 1577. Bibl. Oliveriana,Pesaro.
È solo operando con sistemi di leve e di carrucole reali, e non ideali, e cercando d’individuare i rapporti tra potenza e resistenza, che ci si rende conto che, per ottenere risultati numerici affidabili, occorre operare su sistemi meccanici prima disposti in equilibrio indifferente e poi caricati con i dovuti pesi. L’esistenza dell’equilibrio indifferente diventa una questione di radicale importanza.
10.5.2 Sistemi di carrucole
La questione dell’equilibrio indifferente, oltre alle leve, riguarda le carrucole che Guidobaldo giustamente riconduce alla leva a bracci uguali, cioè alle libre di cui sopra.
Alla carrucola e ai sistemi di carrucole Guidobaldo dedica un intero capitolo, con 28 proposizioni e 17 corollari, nel quale vengono trattate tutte le combinazioni possibili sia di carrucole singole, sia di taglie a due o tre carrucole. Per stabilire con certezza le relazioni tra potenza e resistenza nelle diverse disposizioni Guidobaldo fa costruire, quasi certamente dall’officina urbinate degli strumenti scientifici, sistemi di carrucole estremamente precise, leggere e a bassissimo attrito. In una lettera a Giacomo Contarini
È significativa la cura con cui Guidobaldo realizza i test sperimentali e il benefico intreccio tecnico-matematico che si attiva. Anche se egli non possiede la nozione di momento d’inerzia, tuttavia si rende conto di alcuni effetti dinamici. Ad esempio che le bilance piccole e a bracci leggeri sono molto più sensibili di quelle grandi e a bracci pesanti, conoscenza quest’ultima che egli consapevolmente trasferisce alle carrucole.39
10.5.3 La bilancia idrostatica
Mettendo in relazione i suoi studi sulla “libra” con la tradizione idrostatica archimedea, Guidobaldo espone nelle Meditatiunculae41 un metodo per determinare mediante bilancia ed immersione in acqua, la densità di un corpo. Il problema affrontato è il calcolo della densità relativa (o peso specifico) di un corpo che risulta dal rapporto tra il peso del corpo in aria e il peso del corrispondente volume d’acqua, quest’ultimo misurato tramite la diminuzione del peso del corpo una volta immerso in acqua.
La determinazione della densità di vari materiali—ferro, rame, argento, oro, mattoni, marmo—era stata in precedenza intrapresa, con un procedimento del tutto empirico, dal matematico bresciano Nicolò Tartaglia
La bilancia di Guidobaldo è una leva di primo genere con fulcro in B e con i bracci BC e BD non necessariamente uguali, come del resto è nella stadera.
Infatti Guidobaldo non impone la condizione d’uguaglianza dei bracci BC e BD, gli basta supporre che il corpo A appeso in C di cui si vuole misurare la densità, e il peso E—appeso in D—per bilanciarlo, stiano in equilibrio, qualunque sia la distanza di C e di D dal fulcro B della bilancia. Una volta che il corpo A è immerso in acqua l’equilibrio viene meno. Il peso E viene, quindi, spostato verso il fulcro B fino al punto F, cioè fino al punto in cui si ripristina l’equilibrio. Guidobaldo dimostra che la densità relativa del corpo A corrisponde al rapporto BD/DF delle lunghezze. Se si mantiene la distanza BC fissa, appendendo sempre nello stesso punto il corpo di cui si vuole misurare la densità, questa relazione consente di tracciare sul braccio BD della bilancia una graduazione che indica direttamente i valori della densità. È evidente che con tale disposizione l’apparato diventa uno strumento per misurare una grandezza fisica, cioè una bilancia idrostatica.
È interessante notare la somiglianza della bilancia di Guidobaldo con la Bilancetta, opera giovanile di Galileo
Questa attività sperimentale ci porta ad alcune considerazioni. La libra, i sistemi di carrucole e la bilancia idrostatica, sono tra i primissimi strumenti costruiti da Guidobaldo per verificare e ricercare proprietà fisiche. Egli ha ben chiaro che non è possibile una teorizzazione diretta degli apparati tecnici, e che bisogna procedere ricostruendo in modo opportuno tali apparati in modo da cogliere gli elementi essenziali richiesti dalla teoria, eliminando effetti collaterali. Questa è la “filosofia” della lettera al Contarini
Il Mechanicorum sotto questo aspetto segna l’apertura della grande stagione meccanica seicentesca. Esso non va letto con l’occhio rivolto al dopo, ma piuttosto rivolto a cosa si poteva scrivere in una data “bassa” come il 1577. Ad esempio, per quanto attiene la matematica, è certamente vero che nell’ambito delle tradizionali attività tecniche essa veniva utilizzata più o meno correntemente, tuttavia la sua valenza non era metodologica e costruttiva, bensì ausiliaria, ossia vista come una “tecnica” da affiancare ad altre. Con il Mechanicorum indubbiamente questo secolare status inizia a cambiare. Qualunque sia il giudizio sulla percentuale di originalità dell’opera, resta il merito di essere stato il primo serio tentativo in materia.
10.6 Strumenti per la misura del tempo
10.6.1 Gli orologi solari a rifrazione
Vi sono evidenze documentali che attestano lo studio e la progettazione di Guidobaldo di alcuni particolari orologi solari detti a rifrazione. La più importante fonte storica a riguardo è quella fornitaci da Muzio Oddi
Tra quante cose belle, et ammirabili, che in proposito d’Horologi da Sole sono state ritrovate insino al giorno d’hoggi, nissuna è che per mio credere pareggi quella del farli nel concavo d’un vaso, con si fatto artifitio, che l’ombra non mostri l’hore giuste, se non quando è tutto ripieno d’acqua; non potendosi, non senza meraviglia vedere, che col fare i raggi rinfranti, storcere l’ombra del Gnomone, la dirizzano in parte, che ne faccia conoscere il vero. Chi di così curiosa cosa ne sia stato l’autore, non saprei darne certo notizia, non sapendo che nessuno de gl’Antichi n’habbia lasciato memoria alcuna: ben so de moderni, che l’anno 1572 l’illustrissimo Signor Guidobaldo de Marchesi del Monte ne fece fare uno da Simone Baroccio, eccellente artefice, in una mezza sfera d’Ottone, et hollo havuto nelle mani molto tempo, il quale servì poi come per modello d’uno, che d’ordine del Duca Francesco Maria Secondo, ne fu fabricato entro la tazza della fonte, che è nel giardino pensile del suo magnificentissimo palazzo d’Urbino, come si vede fino al giorno d’hoggi. E circa ai medesimi tempi Gio. Battista Benedetti publicò la sua Gnomonica nella quale [a margine: 1574] fece mentione con un particolare capitolo di questo istesso horologio; et un giorno parlandone io col Padre Christoforo Clavio in Roma, mi disse che Giovanni da Monteregio n’havea fatto uno ancor lui per un Prencipe d’Alemagna. Si conservano ancora presso di me alcuni fogli disegnati dal Commandino , che, per quanto ho potuto conietturare, giva cercando la ragione della varietà de gl’angoli delle refrattioni, non retirandosi uniformemente l’ombre fatte dal gnomone, quando il Sole è vicino all’orizzonte, da quando è alto da terra, benché habbia trascorso intervalli uguali, forse per comporre le tavole a questo effetto, non essendo le medesime, che quelle d’Alazeno e di Vitellione [a margine: Alaz. li. 7 prop. 11. Vitel. li. X prop. 8]. Né il Benedetti, né il Signor Guidobaldo lo fecero, ma solo accennarono il come si haverebbe a fare per comporle, e però la fabrica di questi Horologi, fino adesso, si riduce ad una mera pratica” (Oddi 1638, 99-102) .
Il brano ci fornisce un buon numero d’informazioni sulla storia di questi orologi, nonché sul diretto coinvolgimento di Guidobaldo nella realizzazione di uno di questi. Secondo la testimonianza dell’Oddi
10.6.2 L’orologio a calice
Il brano dell’Oddi
“Non è tazza di Bacco e di Fileno / Quel che là vedi concavo emispero; / Orologio è ch’al sol dimostra il vero, / Se fin’a l’orlo è di bell’onda pieno / Ha dunque doppio il vaso in sé calore, / Poi ch’à labri dà il fonte, agli occhi l’ore.”46
Si trattava quindi di un orologio solare portatile, forgiato a calice, che aveva sulla sua superficie interna sia l’incisione del tracciato delle ore, sia uno stilo fisso, inclinato rispetto al piano orizzontale di un angolo pari alla latitudine del luogo per il quale l’orologio era stato progettato; esso veniva riempito d’acqua fino all’orlo in modo tale che la punta dello gnomone potesse raggiungere la superficie dell’acqua. La descrizione del Baldi

fig. 10.15: Orologio solare a rifrazione attribuito al binomio del Monte-Barocci. Museo Galileo
Esso porta nel coperchio della piccola bussola un disegno floreale, simbolo araldico della famiglia della Rovere. Lo strumento fiorentino era presente nella collezione medicea sin dagli anni 1570–72 (inventario della Guardaroba di Cosimo I), probabilmente dono del duca di Urbino a Cosimo I de Medici. Camerota
10.6.3 L’orologio-fontana a rifrazione
La seconda informazione riportata nel brano dell’Oddi

fig. 10.16: L’orologio solare-fontana del Giardino pensile del Palazzo ducale di Urbino. Soprintend. BB. SS. AA., Urbino.
Come già accennato un orologio-fontana in pietra fa ancora oggi bella vista nel centro del Giardino pensile del Palazzo ducale di Urbino. Sul fondo della vasca, approssimativamente di forma semiellittica, sono ancora visibili le incisioni delle linee orarie, in tutto tredici, dalla undicesima alla ventitreesima ora italica, attraversate dalla linea equinoziale e da quella meridiana. L’intero tracciato, tuttavia, per la sua estensione geometrica non sembra essere quello tipico di un orologio solare a rifrazione52 bensì di un orologio a secco.53 Riempiendo d’acqua il catino della fontana ed osservando ad esempio la linea oraria ventitreesima (quella del tramonto essendo ore italiche) tale linea risulta posizionata immediatamente al di sotto della superficie libera dell’acqua, ossia è molto vicina al bordo del catino, come si vede a destra nella figura. È evidente che su tale linea l’ombra rifratta della punta di un qualsiasi gnomone posto sott’acqua non potrebbe mai arrivare. Alla luce di queste considerazioni54 si può ragionevolmente avanzare l’ipotesi che l’attuale fontana-orologio non sia quella descritta dall’Oddi, ma un’altra, forse già allora posizionata in un diverso luogo del Palazzo.
Riferimenti
Baldi, B. (1914). Gli epigrammi inediti, gli apologhi, le ecloghe. Lanciano: R. Carabba.
Bartoli, C. (1564). Cosimo Bartoli gentil'huomo et accademico fiorentino, del modo di misurare le distantie, le superficie, i corpi, le piante le provincie, le prospettive. Venezia: Francesco Franceschi.
Brahe, T. (1598). Tychonis Brahe astronomiae instauratae mechanica. Wandesburg.
Camerota, F. (2003). Two New Attributions: A Refractive Dial of Guidobaldo del Monte and the “Roverino Compass” of Fabrizio Mordente. Nuncius XVII: 25-37
Castrioti, F. (1564). Della fortificatione della città libri III. Venezia: Rutilio Borgominieri.
Commandino, F. (1558). Federici Commandini urbinatis in Planisphaerium Ptolemaei commentarius. Venezia: Aldo Manuzio.
- (1562). Claudii Ptolemaei liber de Analemmate a Federico Commandino Urbinate instauratus et commentariis illustratus. [...] Eiusdem Federici Commandini liber de Horologiorum descriptione. Roma: Paolo Manuzio.
Digges, L., T. Digges (1571). A Geometrical Practise Named Pantometria. London: H. Bynneman.
Dupré, S. (2003). The Dioptrics of Refractive Dials in the Sixteenth Century. Nuncius XVIII: 39-67
Dürer, A. (1532). Albertus Durerus […] versus e Germanica lingua in Latinam, pictoribus, fabris erariis ac lignariis, lapicidis, statuariis, et vniuersis demum qui circino, gnomone, libella, aut alioqui certa mensura opera sua examinant prope necessarius, adeo exacte quatuor his suarum Institutionum geometricarum libris, lineas, superficies et solida corpora tractauit. Paris: apud Christianum Wechelum.
Favaro, A. (1899-1900). Due lettere inedite di Guidobaldo del Monte a Giacomo Contarini. Atti del Reale Istituto Veneto di Scienze, Lettere ed Arti LIX: 307-310
- (1916). Nicolò Tartaglia e la determinazione dei pesi specifici. Commentarii dell'Ateneo di Brescia
Galilei, G. (1968). G. Galilei, Le opere. Florence: Barbera.
Gamba, E. (1994). Documenti di Muzio Oddi per la storia del compasso di riduzione e di proporzione. Physis XXXI: 799-815
Libri, G. (1838-1841). Histoire des sciences mathématiques en Italie depuis la renaissance des lettres jusqu'à la fin du dix-septième siècle. Paris: Renouard.
Maccagni, C. (1999). La cosmologia di Galileo. In: Principio di secol novo Pisa: Cassa di Risparmio di Pisa 67-93
Monte, Guidobaldo del (1577). Mechanicorum liber. Pesaro: Hieronymum Concordiam.
- (1579). Planisphaeriorum universalium theorica. Pesaro: Girolamo Concordia.
- (1600). Perspectivae libri sex. Pesaro: Girolamo Concordia.
- (1609). Problematum astronomicorum libri septem. Venezia: Bernardo Giunti, Giovanni Battista Ciotti e soci.
Napolitani, P. D. (1988). La geometrizzazione della realtà fisica: il peso specifico in Ghetaldi e in Galileo. Bollettino di storia delle scienze matematiche 2: 139-237
Oddi, M. (1625). Dello squadro trattato di Mutio Oddi da Urbino. Milano: Bartolomeo Fobella.
- (1633). Fabrica et uso del compasso polimetro. Milano: Francesco Fobella.
- (1638). De gli orologi solari trattato di Mutio Oddi da Urbino. Venezia: Ginammi.
Piccolomini, A. (1565 [1545]). In mechanicas quaestiones Aristotelis paraphrasis. Venezia: Traianum Curtium.
Rose, P. L. (1970). Renaissance Italian Methods of Drawing the Ellipse and Related Curves. Physis XII: 399-400
- (1975). The Italian Renaissance of Mathematics. Genève: Droz.
- (1976). Jacomo Contarini (1536-1595) a Venetian Patron and Collector of Mathematical Instruments and Books. Physis XVIII: 117-130
Sangiorgi, F. (1989). Diario di Francesco Maria II della Rovere. Urbino: Quattroventi.
Stevin, S. (1605-1608). Mémoires mathématiques. Leyde: chez Jan Paedts Jacobsz.
Tartaglia, N. (1551). Regola generale da sulevare con ragione e misura non solamente ogni affondata nave, ma una torre solida di mettallo, trovata da Nicolò Tartaglia, delle discipline mathematiche amatore, intitolata la Travagliata invenzione. Venezia: Nicolò Bascarini.
- (1556-1560). General trattato di numeri e misure. Venezia: Curzio Troiano.
- (1560). Quinta parte del general trattato de numeri et misure di Nicolò Tartaglia. Venezia: Curzio Troiano.
Note a piè pagina
Simone, fratello del famoso pittore Federico, è figlio d’arte. Il padre Ambrogio, era un orefice che all’occorrenza “lavorava di cavo e di rilievo modelli, sigilli et astrolabij.”
Nel Proemio alla Fabrica et uso del compasso polimetro Muzio Oddi (1633), parlando di Guidobaldo, afferma che “in quei tempi [1570c.] si tratteneva in Urbino per conferire i suoi studij con il Commandino et spesso era alla casa dove lavorava il Baroccio.”
Orazio del Monte a Galileo, Crema 16 giugno 1610 (Galilei 1968, vol. X, 371).
Cfr. (Monte 1600). In quest’opera non compaiono strumenti prospettici.
Per media grandezza Guidobaldo intende il diametro di un piede, il piede di Pesaro misurava 34 cm.
Circa i materiali più idonei per la costruzione dello strumento Guidobaldo cita il ferro, il bronzo, o il legno duro.
Gemma Frisius, pur riconoscendo che non si tratta di cerchi, parla di curve anomali; De Rojas, invece, le lascia senza nome ma ha il merito comunque di disegnarle in forma corretta per punti.
Si noti che Simone Stevino cita nelle sue Mémoires mathématiques (Stevin 1605-1608, vol. II, libro I) il metodo utilizzato da Guidobaldo e ciò a riprova che le sue opere erano già conosciute ed apprezzate.
Tra i contemporanei che hanno utilizzato il metodo per punti Guidobaldo cita il Dürer e Commandino. Albrecht Dürer aveva descritto nella sua Institutionum Geometricarum (Dürer 1532) un metodo per disegnare le coniche. Lo stesso aveva fatto il Commandino nel De Horologiorum Descriptione e in particolare nella descrizione degli orologi solari orizzontali dove aveva fornito un teorema per disegnare per punti l’ellisse. Ma se Commandino si era limitato a fornire un teorema geometrico il Dürer aveva costruito un vero e proprio apparecchio che a suo dire disegnava ellissi ma che in realtà costruiva curve che si torcevano su se stesse.
Ciascun foro dista, rispetto al cursore più lontano, della lunghezza del semiasse maggiore dell’ellisse.
Per una rappresentazione secondo criteri grafici simili di uno strumento topografico si veda (Castrioti 1564), a riprova della simbiosi nel ducato di Urbino tra ambito tecnico e ambito scientifico, tenuto conto poi che Guidobaldo spesso ricopriva anche mansioni tecniche.
Questo strumento aveva ispirato la costruzione di un particolare compasso da parte di un allievo di Regiomontano, tale Johann Werner (1468–1528), descritto in un libellus del 1522. Probabilmente quest’ultimo apparato aveva ispirato anche quello del Dürer.
Cfr. (Oddi 1638, 183–192; Rose 1970).
Meditatiunculae Guidi Ubaldi ex Marchionibus Montis S. Mariae de rebus mathematicis, Bibliothèque Nationale, Parigi, ms. lat., 10246. Il manoscritto è una sorta di zibaldone contenente scritti su svariati argomenti di matematica e fisica. E’ databile all’incirca al periodo 1587–92. Alcune parti del manoscritto sono state pubblicate da Libri (1838-1841, vol. IV). I disegni con le descrizioni si trovano nel vol. IV, pp. 380–383, da cui sono tratte le immagini sopra riportate.
Ibidem, cc. 7–8.
Cfr. (Commandino 1562, ff. 58v-59v).
Ms. cit., cc. 9–11.
Ibidem, c. 12. Il titolo è Misurar a lo squadro tagliato in otto parti, questa pagina è riprodotta in (Libri 1838-1841, vol. IV, 384-392).
Nelle collezioni medicee presso il Museo Galileo di Firenze, è conservato uno squadro marcato “Urbino 1654,” che oltre alle fenditure a 90° e 45° ha una fenditura a 30°/60°.
I primi squadri erano dei dischi in legno con due fenditure ad angolo retto. Tartaglia, ancora nella terza parte del terzo libro del suo General trattato di numeri e misure (Tartaglia 1556-1560) descrive il modello piatto munito di forellini o traguardi alle estremità dei due diametri ortogonali.
Guidobaldo precisa che se la misura avvenisse in un terreno non pianeggiante: “Guardisi per le spaccature la sommità del monte facendo star lo squadro sempre retto all’horizzonte,” Meditatiunculae, ms. cit., c. 12.
Cfr. (Digges and Digges 1571), pubblicato postumo dal figlio di Leonard, Thomas Digges.
Un apparato simile, tra i più antichi conosciuti, era stato già descritto nella Margarita philosophica di Gregor Reisch del 1512. Lo strumento, denominato polimetrum, venne descritto in appendice al testo dal topografo e cartografo renano Martin Waldseemüller. Alla stregua dello strumento di Guidobaldo esso misurava angoli orizzontali e verticali ma il suo uso era rivolto essenzialmente al rilevamento e alla cartografia.
Brahe (1598) descrive con grande cura tutto l’armamentario strumentale di Tico. Esso era caratterizzato da scale graduate di grandi dimensioni e da soluzioni tecniche avanzatissime quali, ad esempio, l’uso di precisi sistemi di traguardo a doppia fenditura: un modus operandi ben diverso rispetto a quello scelto da Guidobaldo.
Come già ricordato i Problematum si aprono proprio con la lettura delle scale graduate e con il metodo delle frazioni di grado.
Quest’aspetto si integra bene con il largo disinteresse da parte degli artefici urbinati degli strumenti scientifici verso la costruzione di strumenti astronomici.
Si vedano, ad esempio, i successivi compassi di Galileo, Coignet e di altri tra cui il modello dello stesso Muzio Oddi (1638).
Si vedano nel primo libro dei Problematum astronomicorum rispettivamente i problemi I, III, IV, V, ff. 2v–6v.
Si noti che non fa alcun cenno al problema della realizzazione tecnica delle graduazioni delle scale, sembra che dia per acquisita la loro buona divisione.
Cfr. Op. cit., ff. 5r–6v.
Cfr. (Monte 1579, 38). Un appunto sul metodo generale di calcolo della frazioni di grado compare anche a c. 109 del citato manoscritto parigino delle Meditatiunculae.
A quanto pare Contarini aveva inviato a Guidobaldo l’apparato su cui il marchese aveva modellato uno suo. Egli, quindi, chiede al Contarini il permesso di descrivere il meccanismo nel suo quasi pronto Problematun astronomicorum opera che poi uscirà postuma senza alcun accenno al Contarini. Per l’intera vicenda cfr. (Rose 1975, 224); G. del Monte a G. Contarini, Pesaro 4 gennaio e 15 febbraio 1580, in (Rose 1976, 127).
Di questo meccanismo se ne è tuttavia conservato il principio. Si pensi agli strumenti per l’amplificazione di grandezze lineari (spessori, scentrature,…), quali, ad esempio, il comparatore o minimetro, tuttora in uso presso i tornitori, dove, sempre tramite ingranaggi, allo spostamento di un’asta di 1 mm risponde la deviazione di un indice su un quadrante di 100 divisioni.
Galileo non mostra apprezzamento per la cospicua impresa strumentale del Brahe, e arriva perfino ad affermare di aver ottenuto buone misure del diametro apparente delle stelle traguardando a occhio nudo la collimazione tra le stelle e una corda tesa, cfr. G. Galilei, Dialogo sopra i due massimi sistemi (Galilei 1968, vol. VII, 388-389). In generale cfr. (Maccagni 1999).
Cfr. il cap. I, prop. IV, del Mechanicorum che da sola occupa ben 51 pagine.
G. del Monte a G. Contarini, Pesaro 9 ottobre 1580, in (Favaro 1899-1900).
La questione compare già nei Problemi meccanici aristotelici, cfr. (Piccolomini 1565 [1545], quest. 9, 852a).
G. del Monte a G. Contarini, lett. cit. (Favaro 1899-1900, 307).
Meditatiunculae, ms. cit., c. 232. Il titolo dei tre fogli consecutivi dedicati al problema recita: “Gravitatum proportionem cuiuslibet gravis, humido gravius, ad humidum, libra notam reddere.”
Cfr. (Tartaglia 1551) fogli non num., “secondo ragionamento” (Favaro 1916; Napolitani 1988).
Meditatiunculae, ms. cit., c. 234. Cfr. (Galilei 1968, vol. I, 219-220).
Di questo costruttore si conoscono solo tre strumenti molto simili tra loro: due di questi, datati 1547, sono in Spagna rispettivamente presso il Museo de Santa Cruz di Toledo e presso il Museo Nacional de Ciencia y Tecnologia di Madrid; il terzo, datato 1548, è conservato presso la Collection of Historical Scientific Instruments della Harvard University.
Dupré ipotizza che il Commandino venne stimolato su questi argomenti dall’Ausonio; in effetti entrambi studiarono medicina a Padova tra il 1540 e il 1545 ed ebbero rapporti con l’Accademia della Fama. La loro diretta conoscenza è comprovata da un paio di lettere conservate presso la biblioteca Ambrosiana di Milano.
(Baldi 1914). L’epigramma citato è il n. 375, vol. I, p. 82. L’esistenza dell’opuscolo di Guidobaldo sugli orologi solari a rifrazione è confermata anche da una nota in un manoscritto anonimo di architettura militare, cfr. BOP, ms. 198, c. 146v.
La notizia è riportata in (Gamba 1994, nota 34). Gli oggetti di Guidobaldo, ed in particolare l’orologio, vennero contrattati per l’acquisto da Muzio Oddi. Scrive l’Oddi al Giordani: “Già scrissi al signor Piermatteo che vedesse di recattare tutti quei libri che erano del signor Guidobaldo, e si comprassero a conto mio a ogni prezzo, e così anco i suoi strumenti e particolarmente quell’horologio coi raggi rinfranti, desiderarei ancora qualche aviso di ciò che si può sperare del feudo di Monte Baroccio,” Lucca, 6 settembre 1634, lettera di Muzio Oddi a Camillo Giordani, Biblioteca Oliveriana, Pesaro, ms. 413, cc. 231r–231v.
Le predette assenze furono dovute per buona parte all’accumulo di vari contenziosi giudiziari con il duca che gli procurarono carcerazione ed esilio dal 1601 al 1637.
L’occasione probabilmente potrebbe essersi presentata per la rottura del sistema idrico del giardino pensile che alimentava la suddetta fontana.
Il Baldi era un esperto di orologi solari, sui quali aveva scritto un trattato, se la trasformazione fosse già avvenuta probabilmente l’avrebbe segnalata.
A proposito di Francesco Maria II, Alexander Marr ha recentemente segnalato una lettera di Muzio Oddi inviata prima dell’agosto del 1612 a Pier Matteo Giordani nella quale lo scienziato urbinate, oltre a manifestare l’intenzione di voler pubblicare l’opuscolo Degl’horologi coi raggi rinfranti nell’aqua scritto da Guidobaldo—intenzione mai realizzata per l’opposizione del figlio di Guidobaldo, Orazio—, afferma che Guidobaldo inventò quegli orologi “per servire al serenissimo nostro Padrone,” cioè Francesco Maria II; cfr. Biblioteca Oliveriana, Pesaro, ms. 413, cc. 7r–8v.
A questo proposito è sufficiente analizzare gli orologi dell’Hartmann per rendersene conto.
Su questo importante aspetto siamo debitori all’astronomo Lino Colombo per averci fornito adeguate informazioni a riguardo.
A nostra conoscenza, fino ad oggi, si è sempre identificato l’attuale orologio-fontana del giardino pensile con quello descritto dall’Oddi nel brano del 1638.
