1. Nel trattato De prospectiva pingendi Piero della Francesca
Così, allo stesso modo, Guidobaldo del Monte nel primo dei Perspectivae libri sex subito presenta un’analoga tripartizione della pittura che definisce con i seguenti termini: “delineatio, umbra et colores” (Monte 1600, 2). Ugualmente il discorso specifico dell’autore si rivolge solo alle prime due parti perché rientrano sotto il dominio della prospettiva, quindi tali da costituire riferimento oggettivo e solida base alla disciplina e non per ultimo in grado di conferire superiore dignità a chi la esercita.
La tangibile ascendenza pierfrancescana è attenuata dalla variante del secondo termine, “l’ombra” al posto di “commensuratio.” Il vocabolo adottato da Piero
In base ad un’antica tradizione, tramandataci da autori come Quintiliano,2 Plinio il Vecchio3 e Atenagora,4 l’invenzione della pittura è collegata al tracciato sulla parete di una figura seguendo il contorno dell’ombra proiettata da un corpo umano illuminato da una sorgente di luce.
L’idea del breve cono d’ombra proiettato dai corpi opachi si applica a grandezze spaziali progressivamente crescenti, fino alla profondità degli spazi eterei, in cui si proiettano i coni d’ombra che la Terra e la Luna generano determinando il verificarsi delle eclissi.
Frattanto, nella Grecia classica gli antichi raggiunsero una convincente spazialità nella rappresentazione. Da un esame attento e da un confronto serrato tra i passi delle fonti letterarie che ricordano Apollodoro d’Atene, si afferma esplicito il suo valore sia come σκιαγράφος, sia come σκηνογράφος, quindi prospettico e al tempo stesso pittore di ombre.5 Con ogni verosimiglianza nella distinzione e simultanea compresenza dei due elementi tecnici e stilistici consiste la singolarità della sua personalità artistica. Gli si dà l’epiteto di σκιαγράφος6 e gli si riconosce altresì il merito di “exprimere species,” “rappresentare, dar forma all’apparenza visibile.”7 Vale a dire che specificamente nella locuzione “pittore di ombre” il secondo termine assume la duplice valenza di “parvenze,” “figure illusorie” ed anche, al fine della simulazione del vero, di ombre “primitive” e “derivative” secondo la terminologia leonardiana e che noi chiamiamo rispettivamente ombre “proprie” o aderenti ai corpi e ombre “portate” o “proiettate.” Nel suo significato complessivo è legittimo il riferimento così alla realtà visiva e alla verità ottica, come alle apparenze sensibili, agli inganni, alle illusioni resi attraverso il consapevole e abile impiego degli artifici del disegno, della composizione, del colore unito alla luce.
Il ricorrere delle medesime costanti formali induce ad avanzare significative consonanze fra le vicende della storia artistica antica e di quella moderna, tali che ognuna delle due può illuminare l’altra. Per via delle comuni e determinanti basi prospettiche, il singolare svolgimento della pittura greca nella seconda metà del quinto secolo si accosta perfettamente allo sviluppo organico nella pittura del Quattrocento italiano.
Quando alla fine del secolo l’attività di Apollodoro giunge al suo apice, era trascorso un cinquantennio dalle prime invenzioni di prospettiva dipinta da parte di Agatarco, pittore cui appartengono le scene per una delle tragedie di Eschilo,8 composte secondo gli artifici della geometria che davano all’immagine visiva la sensazione illusoria della profondità. All’incirca lo stesso lasso di tempo che intercorse durante il Rinascimento tra i due esperimenti brunelleschiani di vedute urbane fiorentine in prospettiva e i frutti definitivi nella pittura prospettica conseguiti da Piero della Francesca
Una concordanza puramente visuale che indica con chiarezza il comune orientamento formale.
Nell’incisiva valutazione della sua arte, il senso comune ai succinti passi delle fonti è che il merito di Apollodoro consiste nella novità di rappresentazione della realtà ottica, non tanto con il tracciato lineare dei contorni per disporre le forme nello spazio, perché Agatarco ne era stato il precursore e l’iniziatore nella scenografia teatrale, quanto con la modulazione e la gradazione dei colori materiali per la resa dei valori della luce e dell’ombra.9 Si potrebbe dire “sintesi prospettica di forma e di colore,” secondo l’essenziale ed efficace espressione coniata dall’illustre storico d’arte Roberto Longhi
Prendo un solo esempio figurativo pierfrancescano che venga ad assicurare e dimostrare l’unità di universo formale e suppongo che consenta di sintetizzare l’accostamento. Nella cosiddetta pala di Brera un’ambivalenza intrinseca all’immagine lega in efficace accordo scenario architettonico, disposizione dei personaggi e distribuzione d’ombre e luci, facendo sì che l’apparenza visiva contraddica e sovverta l’ordinamento reale delle cose (Maltese 1974)
Per via della prospettiva la pittura compone cose finte, ma formate a somiglianza del vero. Essa diviene così un prodigioso strumento di sostituzione del reale che si avvale del rapporto ambivalente tra verità e illusione, tra realtà e finzione.
Con Leon Battista Alberti
Vediamo dunque d’indagare alcuni tratti caratteristici del meccanismo che rende possibile l’illusione visiva, i quali non esito a definire propri della scuola prospettica urbinate.
2. Ai fini di un’interpretazione unitaria dell’arte o scienza della prospettiva durante il Rinascimento funge da elemento ordinatore lo svolgimento lento e graduale dalla regola del punto principale, o punto di fuga delle rette perpendicolari al quadro, al concetto di punto di fuga nel senso più generale e completo del termine, introdotto proprio da Guidobaldo del Monte. Spetta a lui infatti il riconoscimento della fondamentale proprietà che in prospettiva l’immagine di un qualunque sistema di rette parallele fra loro, ma non al quadro, è un fascio di rette concorrenti nel punto ove la retta condotta per l’occhio, ad esse parallela, interseca il quadro stesso.
Una delle tappe salienti di questo processo evolutivo è la costruzione nella quale Piero della Francesca
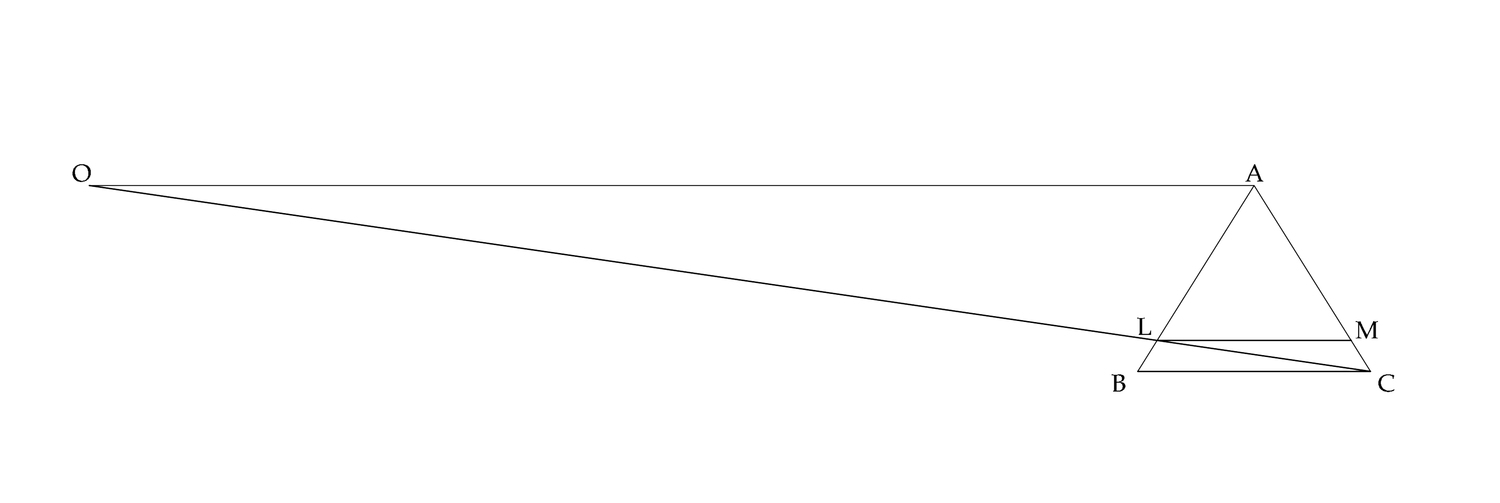
fig. 8.1: La prospettiva di un quadrato ottenuta da Piero della Francesca
Si tratta del procedimento detto con “punto di distanza,” perché la “distanza” tra i due punti corrisponde esattamente alla “distanza” dell’osservatore dal quadro (Piero 1942, 87
Alla stregua di un artificio tecnico il nuovo elemento costruttivo entra nell’uso della pratica figurativa, tanto che la storia prospettica suole a proposito indicare una linea genealogica di discendenza che collega Piero della Francesca
L’impulso decisivo in tal senso si deve all’indagine analitica di Guidobaldo del Monte che nella proposizione XX del secondo libro dà l’elaborazione teorica e l’esemplificazione pratica del modo di procedere seguito da Piero della Francesca
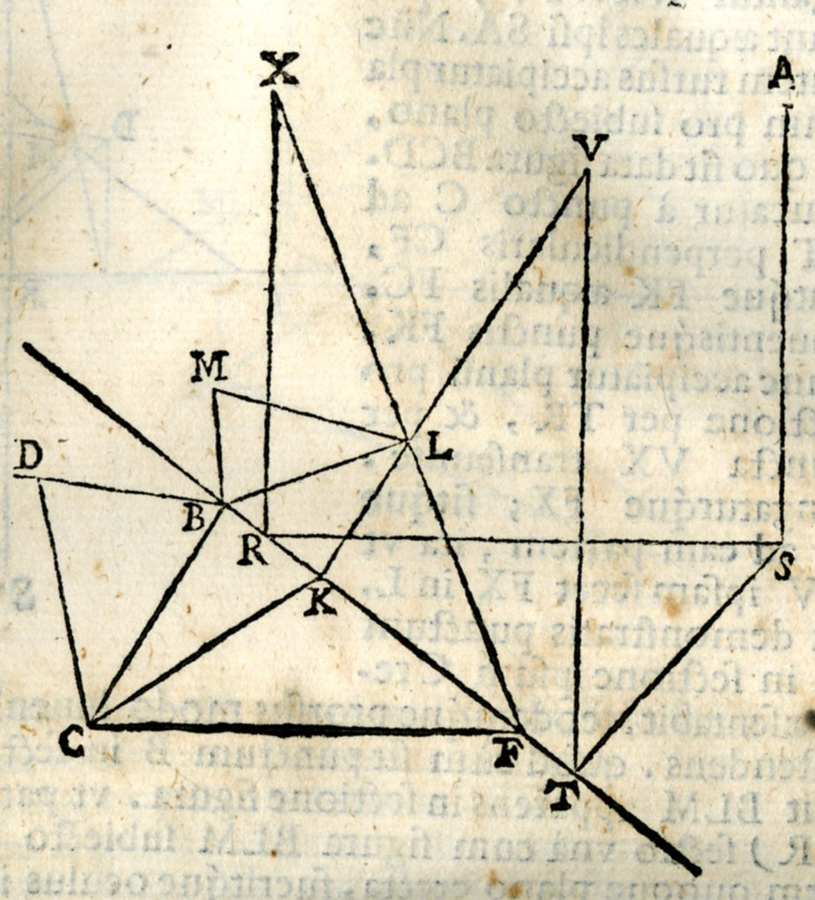
fig. 8.2: Decimusquintus modus (foto Biblioteca Oliveriana, Pesaro)
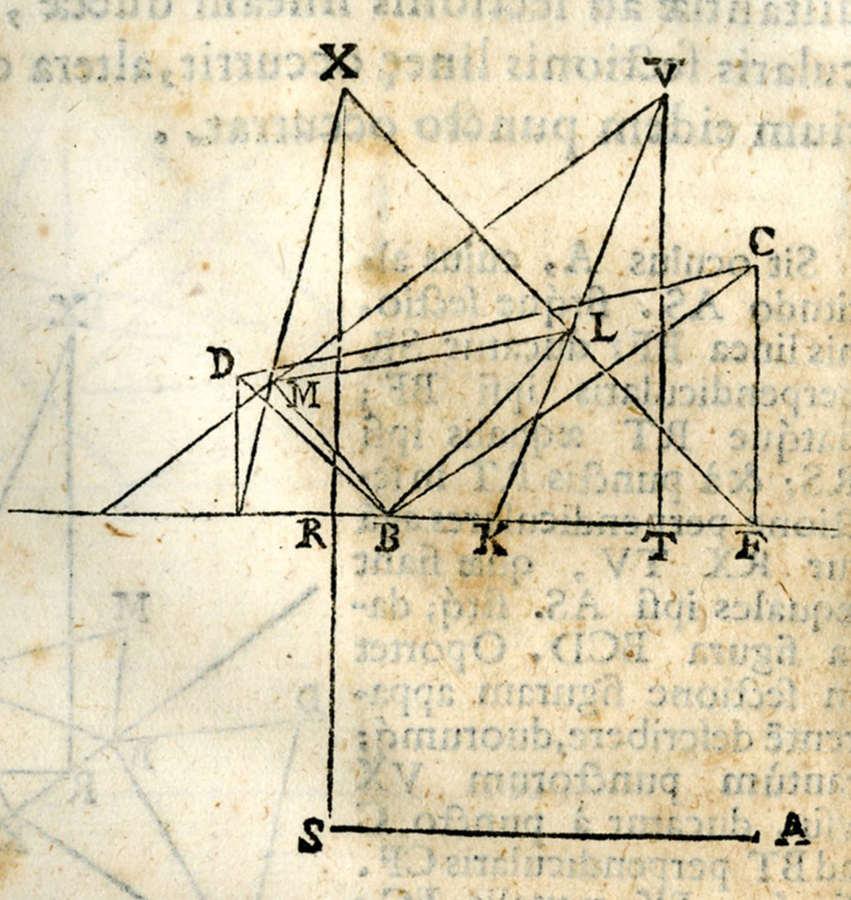
fig. 8.3: Decimusquintus modus (foto Biblioteca Oliveriana, Pesaro)
Scelgo principalmente l’elaborazione teorica per determinare con maggior precisione gli elementi che spiegano in modo sostanziale l’accostamento.
È cosa superflua osservare che mentre l’esempio pierfrancescano verte sulla figura apparente del quadrato BCLM, quello di Guidobaldo riguarda invece la figura triangolare BCD, poiché in entrambi vi è l’esigenza prioritaria di trovare la prospettiva L del singolo punto C. È proprio la comune finalità a divenire valida base di confronto fra i disegni di Piero della Francesca
La correlazione degli elementi nel sistema e l’integrazione dinamica tra gli spazi esterno ed interno al quadro si attuano attraverso le coppie di rette parallele RX TV, SR FC, ST KC, che sono o perpendicolari o inclinate a 45o rispetto alla linea di sezione. Così nella sezione eretta al piano sottostante le immagini delle rette date concorrono nei punti centrale X e laterale V, alti quanto l’occhio, e s’intersecano in L, prospettiva del punto dato C (Figura 8.3).
Innanzitutto, riguardo alla nomenclatura, segnalo che Guidobaldo chiama “sectio erecta” il quadro verticale e “subiectus planus” il piano orizzontale terreno o geometrale, con il termine “sectionis linea” intende l’intersezione del quadro con il geometrale ovvero la linea di terra o retta fondamentale e invece attribuisce il nome di “punctus distantiae” all’odierno punto di stazione ovvero al piede della perpendicolare abbassata dall’occhio al piano orizzontale.
Rivolgo poi l’attenzione ad un dato particolare che costituisce la prova evidente della convergenza proposta fra i testi chiamati in causa. Nel “decimusquintus modus” di Guidobaldo il punto laterale V equivale tanto all’“ochio dato” della proposizione XXIII nel I libro del trattato pierfrancescano quanto alla “vista del riguardante” nella seconda regola del Vignola
Proprio l’elevato livello di astrazione dell’analisi fa risaltare indirettamente quegli stessi rapporti logici che soli danno forma e senso all’unità sistematica e funzionale delle parti nel tracciato prospettico presentato assai prima in modo così conciso e circoscritto da Piero della Francesca
Non intendo addentrarmi ulteriormente nel distinguere in modo dettagliato i vari momenti della dimostrazione. Preferisco citare per disteso l’elaborazione teorica lasciando ad una sequenza grafica (Figure 8.6–8.9) il compito di illustrare la serie delle fasi e le ragioni della geometria che il procedimento comporta e implica:
Oculo dato, dataque in subiecto plano rectilinea figura, in proposita sectione subiecto plano erecta figuram apparentem describere. Oporte atque rursus problema perficere duobus punctis in sectione positis ut oculus aeque altis ac ita constitutis ut, ductis perpendicularibus ad sectionis lineam, pars sectionis lineae intercepta sit aequalis lineae perpendiculari a puncto distantiae ad sectionis lineam ductae et, ubi haec perpendicularis sectionis lineae occurrit, altera quoque perpendicularium eidem puncto occurrat. Sit oculus A, cuius altitudo AS, sitque sectionis linea BF. Ducatur SR perpendicularis ipsi BF fiatque RT aequalis ipsi RS et a punctis RT in sectione perpendiculares agantur RX TV, quae fiant aequales ipsi AS. Sitque data figura BCD. Oportet in sectione figuram apparentem describere duorumque tantum punctorum VX usu. Ducatur a puncto C ad BT perpendicularis CF fiatque FK aequalis FC. Oportet autem punctum K ad eam partem collocare, ita ut ductis KV FX se invicem secare possint, ut in L. Dico primum punctum C apparere in L; iunctis enim ST CK, quoniam in triangulo SRT latera RS RT sunt aequalia, erunt anguli RST RTS inter se aequales et, quoniam tres anguli trianguli duobus sunt rectis aequales et angulus SRT est rectus, erit unusquisque angulus RST RTS recti dimidius. Similiter trianguli CFK angulus CFK est rectus et latera KF FC inter se sunt aequalia, unde aequales sunt anguli FCK FKC et unusquisque est recti dimidius. Ergo angulus KTS est angulo TKC aequalis ac propterea linea ST est ipsi KC parallela. Quia vero in sectione linea TV est ipsi TB perpendicularis et ipsi AS aequalis, erit punctum V punctum concursus ipsius KC. Quare linea KC in KV apparet. Cum autem SR CF sint ipsi TB perpendiculares, erunt inter se parallelae, quodcum SR ipsi CF aequidistet et in sectione linea RX sit ipsi TB perpendicularis et ipsi AS aequalis, erit punctum X punctum concursus ipsius FC. Quare CF apparet in sectionem in FX. Et est punctum C in utraque linea KC FC, ergo apparebit punctum C in L, ubi nempe KV FX se invicem secant. Parique ratione invenietur punctum M ipsum D repraesentans et quoniam punctum B est in sectione, iunctis BL LM MB, erit BLM in sectione apparens figura. Quod facere oportebat (Monte 1600, 88–89).
Segue la traduzione (Sinisgalli 1984, 96–97)
Dato l’occhio e data nel piano sottostante una figura rettilinea, disegnare in una assegnata sezione, eretta al piano sottostante, la figura apparente. Bisogna risolvere, di nuovo, il problema con due punti presi in sezione, alti quanto l’occhio; ma in modo tale stabiliti che, tirate le perpendicolari alla linea di sezione, la parte della linea di sezione, intercettata, sia uguale alla perpendicolare condotta dal punto di distanza alla linea di sezione, e dove questa perpendicolare incontra la linea di sezione, anche nel medesimo punto la incontri l’altra perpendicolare (Figura 8.6). Sia A l’occhio, e la sua altezza sia SA, e sia BF la linea di sezione; si conduca SR perpendicolare alla stessa BF e sia RT uguale alla stessa RS; e dai punti RT si mandino in sezione le perpendicolari RX TV, uguali alla stessa AS; e sia BCD la figura data. Bisogna disegnare nella sezione la figura apparente, e servirsi solamente dei due punti VX (Figura 8.7). Dal punto C si conduca CF, perpendicolare a BT; e sia FK uguale ad FC. Bisogna collocare, altresì, il punto K in modo tale che KV ed FX, una volta tracciate, si possano intersecare, ad esempio in L (Figura 8.8). Dapprima, dico che il punto C appare in L; congiunti, infatti, ST e CK, poiché nel triangolo SRT i lati RS ed RT sono uguali, saranno anche uguali gli angoli RST ed RTS; e poiché i tre angoli di un triangolo sono uguali a due angoli retti e l’angolo SRT è retto, si avrà che ciascuno degli angoli RST ed RTS sarà la metà di un angolo retto. Similmente, l’angolo CFK del triangolo CFK è retto e i lati KF ed FC sono uguali tra di loro; per cui, sono uguali gli angoli FCK ed FKC; e ciascuno di essi è la metà di un angolo retto; dunque, l’angolo KTS è uguale all’angolo TKC; e perciò la linea ST è parallela alla stessa KC; e poiché la linea TV in sezione è, altresì, perpendicolare alla stessa TB ed uguale ad AS, il punto V sarà il punto di concorso della stessa KC (Figura 8.9). Per la qual cosa, la linea KC appare in KV. Essendo poi SR e CF perpendicolari alla stessa TB, saranno tra di loro parallele; e poiché SR è equidistante alla stessa CF, e in sezione la linea RX è perpendicolare alla stessa TB ed è uguale alla stessa AS, il punto X sarà il punto di concorso della stessa FC; per la qual cosa, CF appare in sezione in FX. Ma il punto C appartiene sia a KC che ad FC; dunque, il punto C apparirà in L, dove precisamente si intersecano le linee KV ed FX; e, per il medesimo motivo, si troverà il punto M che rappresenta lo stesso D; e poiché il punto B è nella sezione, congiunti i punti BL LM MB, sarà BLM la figura che appare in sezione. Cosa che bisognava fare.
Guidobaldo del Monte non dimentica o consapevolmente tralascia le esperienze prospettiche degli artisti teorici del Rinascimento, ma le contiene in sé e, pur non evocandole mai in modo esplicito, le conduce a un più alto grado di concezione astratta. Nel momento stesso in cui si accinge a sancire il definitivo superamento del procedimento tradizionale, indugia nel sottoporlo ad un altrimenti arduo processo di razionalizzazione. Contribuisce così a conferire ad esso il suo pieno senso.
Nell’estesa esemplificazione del II libro la differenza radicale è che, per trovare la figura prospettica di una figura data, Guidobaldo si era avvalso di due punti qualsiasi di concorso “in sectione positis ut oculus aeque altis” e non si era affidato al solo punto principale e a un punto della distanza come gli autori che lo avevano preceduto.11
3. Abbiamo visto quanto conti, nell’analisi del testo, l’aver rilevato che, in prossimità di una svolta storica e culturale di notevole portata, oltre ad introdurne di nuovi, Guidobaldo del Monte si sia intrattenuto a studiare i più antichi procedimenti che sono riveduti e formulati in termini geometrici rigorosi. Vale quindi la pena dedicare qualche altra veloce riflessione sull’argomento.
Ritengo per esempio assai significativo ed anche sintomatico che il matematico pesarese nel problema immediatamente successivo (libro II, proposizione XXI) illustri il modo per trovare la figura prospettica del triangolo facendo uso di due punti di concorso laterali o di distanza (si vedano le Figure 8.4 e 8.5) (Monte 1600, 91–93).
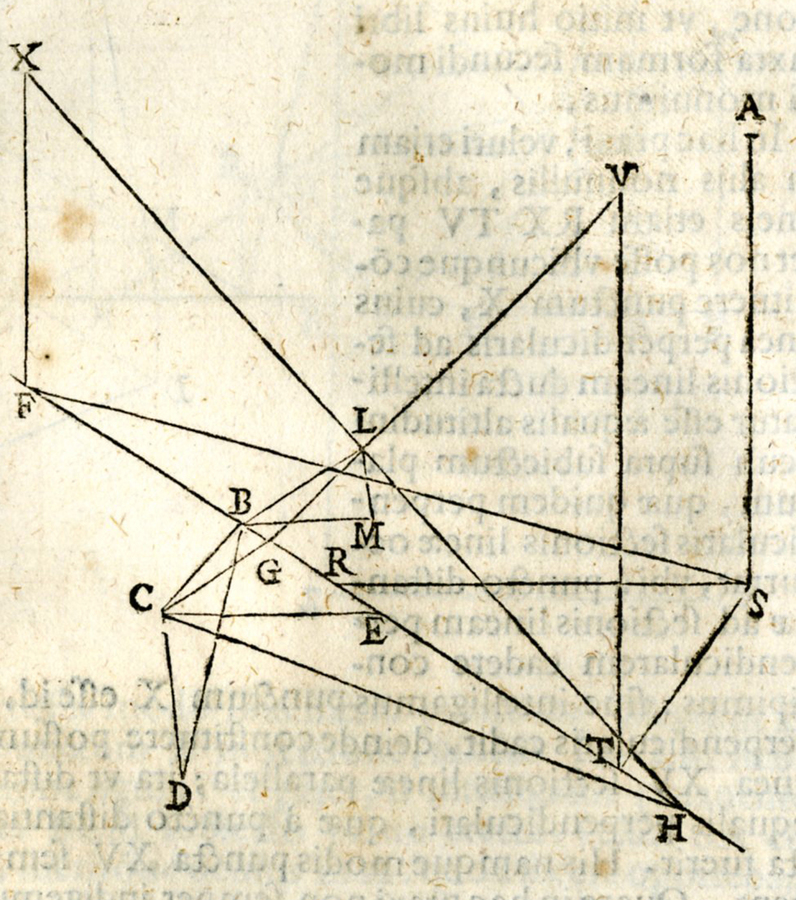
fig. 8.4: Decimussextus modus (foto Biblioteca Oliveriana, Pesaro)
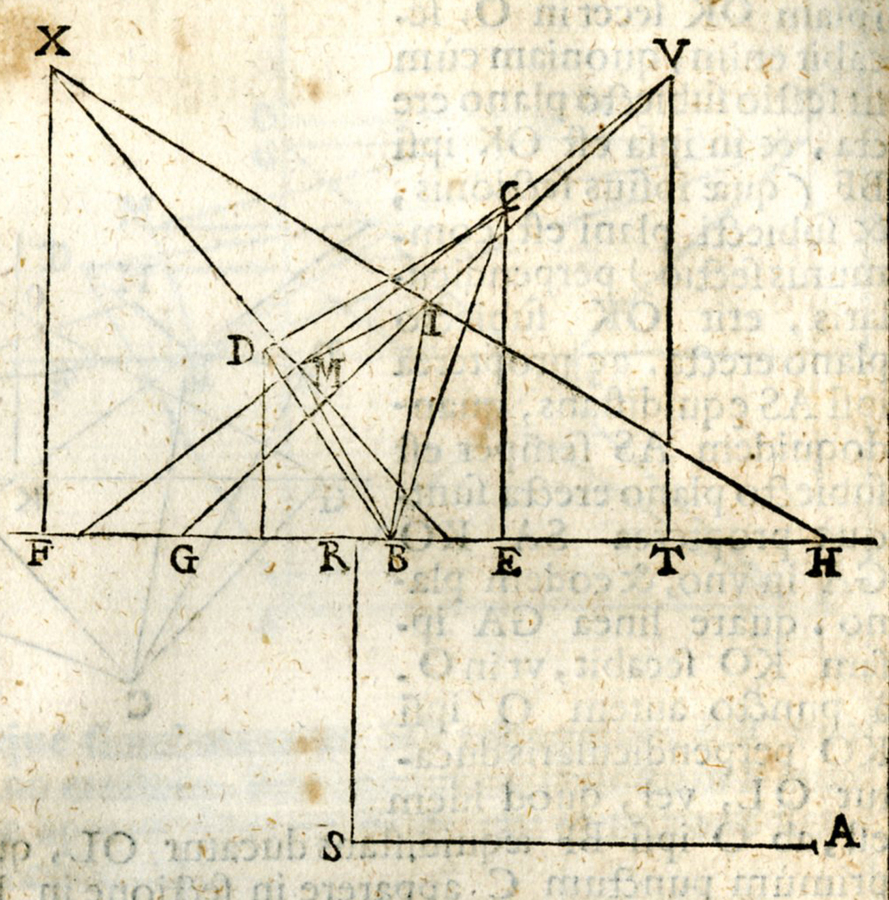
fig. 8.5: Decimussextus modus. Praxis (foto Biblioteca Oliveriana, Pesaro)
Si tratta del metodo cosiddetto bifocale e comunemente considerato in contrapposizione con il modo albertiano. Fu soprattutto la critica di matrice storico-artistica che nella seconda metà del Novecento ritenne di poter annettere casi particolari di formule disegnative accertate innanzitutto in opere figurative del Trecento italiano, ma poi diffusesi anche oltralpe, ad applicazioni del metodo con punti marginali, a cui si attagliava l’uso di espressioni di comodo come “prassi di bottega” oppure “tradizione artigianale,” dato il carattere empirico attribuito alle procedure.
La premessa di una siffatta interpretazione è da individuare nella suggestione esercitata in particolare dopo il ‘50, nella seconda fase della sua influenza, dal saggio La prospettiva come “forma simbolica” di Erwin Panofsky (1892–1968) (Panofsky 1927)
Consapevoli sviluppi applicativi delle tesi panofskiane possono essere considerati i tentativi irrisolti di ricondurre il procedimento con due punti laterali, o metodo bifocale, ad un sistema fondato su principi e criteri diversi e alternativi rispetto a quelli della prospettiva ufficiale, in grado di tener conto e implicare nella costruzione fattori considerati non evitabili come la visione binoculare o la rotazione dell’occhio oppure la visione nel tempo.12
Su questi presupposti è ovvio che seguissero valutazioni antitetiche di due diverse tendenze: l’una interessata al modo speculativo e astratto della prospettiva artificiale, l’altra legata a differenti schemi anche empirici e più approssimati, ma volti a rendere comunque in maniera duttile e aperta i caratteri della visualità naturale. Nel clima culturale dell’epoca la prima, per la sua natura esclusiva, veniva reputata angustamente conservatrice e quindi retriva, la seconda invece, eterodossa e più libera, era considerata innovativa e perciò moderna e progressista.
L’analisi oggettiva e il confronto di entrambe le costruzioni affiancate—il metodo con punto di distanza di matrice pierfrancescana e il metodo bifocale—che Guidobaldo del Monte ha condotto ricostruendone in ogni fase e in tutte le parti la dinamica interna, dimostrano in modo inequivocabile l’assoluta identità tanto dei principi teorici quanto della procedura genetica (Figure 8.6–8.9 e 8.10–8.13).
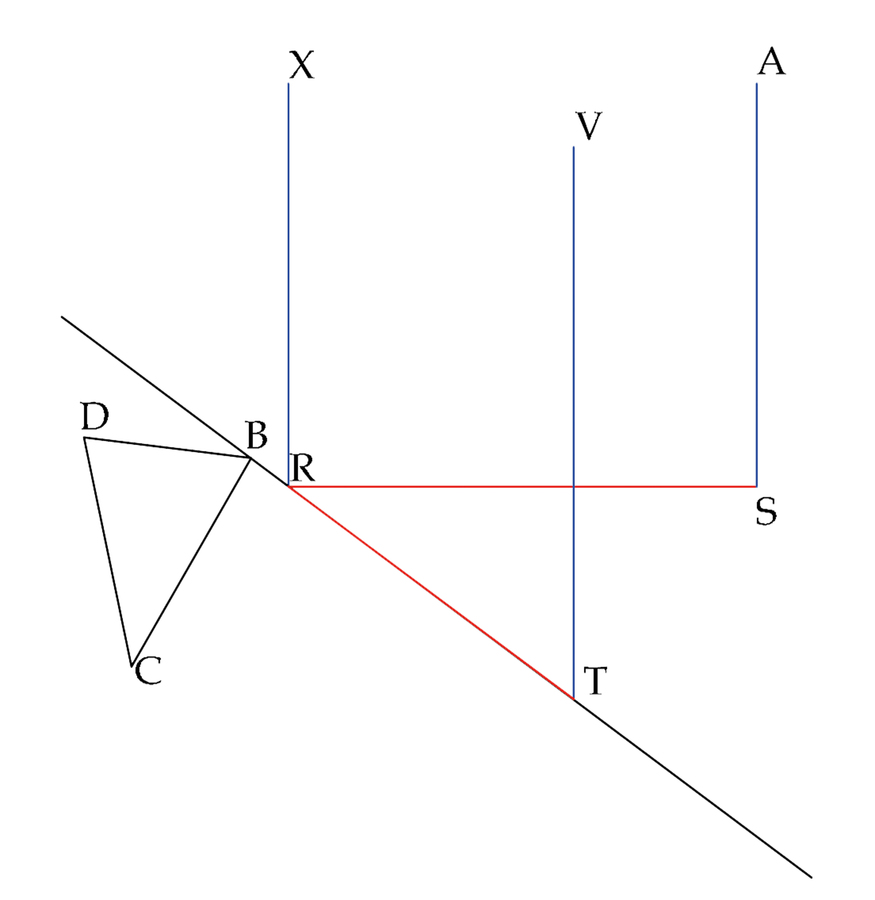
fig. 8.6: La successione delle fasi costruttive nel modo decimoquinto (v. anche Figure 8.7–8.9, disegni di Filippo Parroni). SA = RX = TV. SR è perpendicolare a BT e RT = RS.
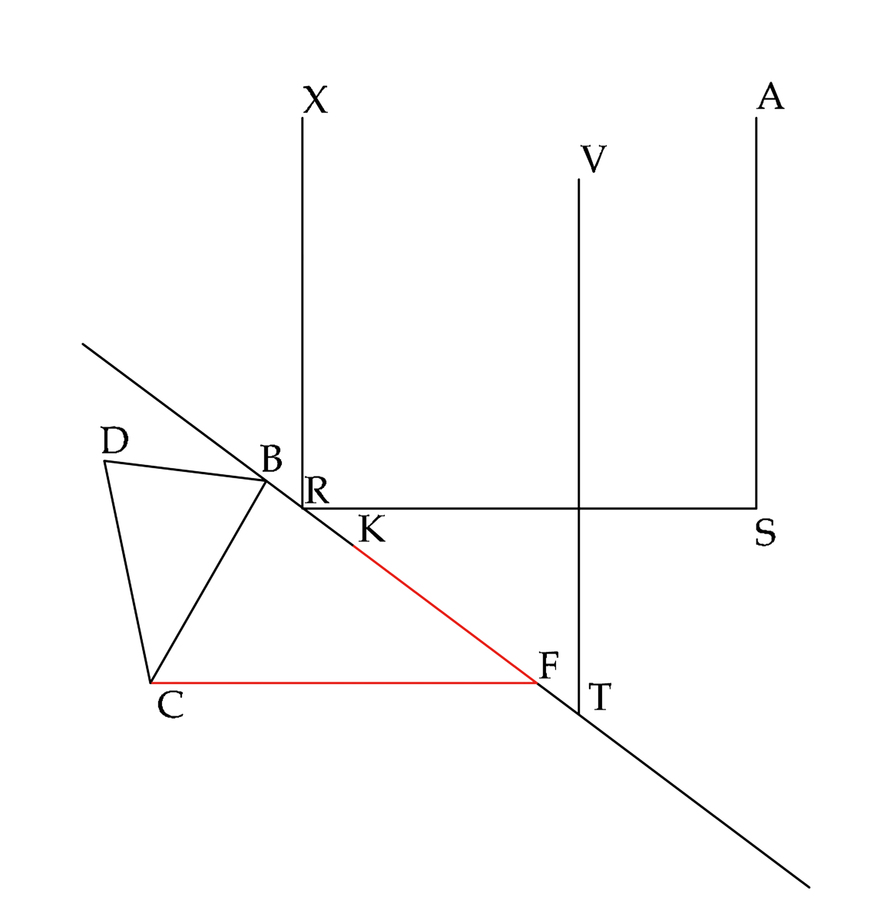
fig. 8.7: La successione delle fasi costruttive nel modo decimoquinto. Allo stesso modo CF è perpendicolare a BT e FK = FC.
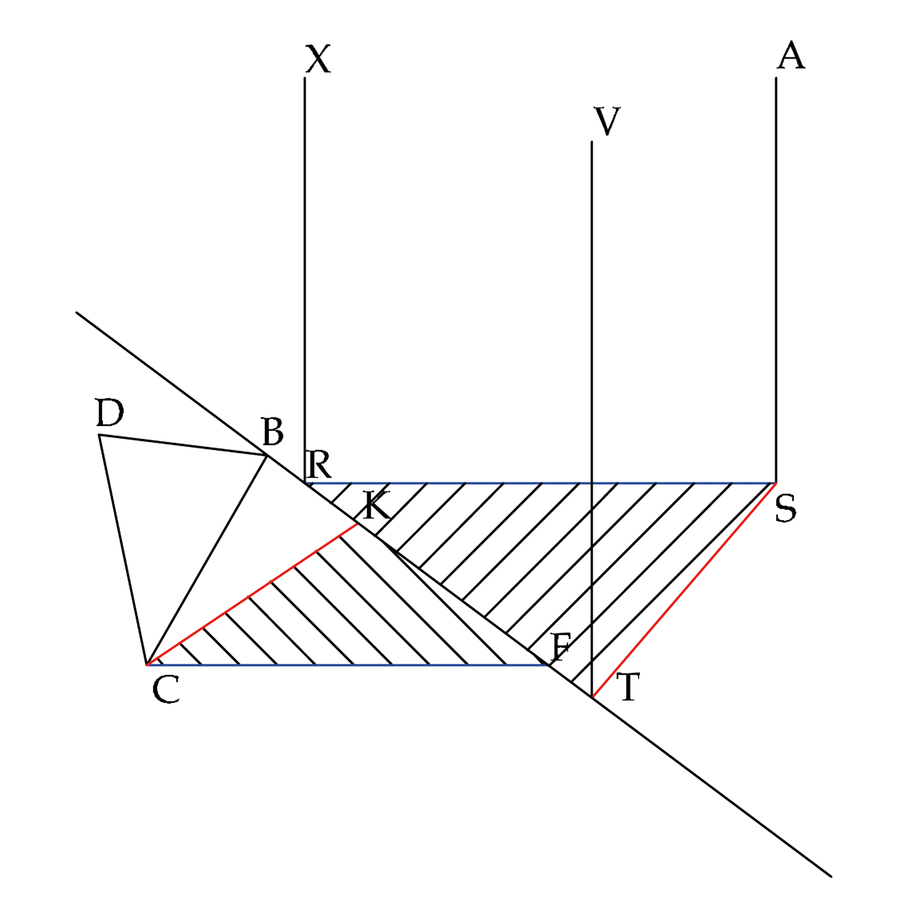
fig. 8.8: La successione delle fasi costruttive nel modo decimoquinto. I triangoli SRT e CFK sono quindi isosceli. Consegue che ST è parallela a KC e SR a CF.
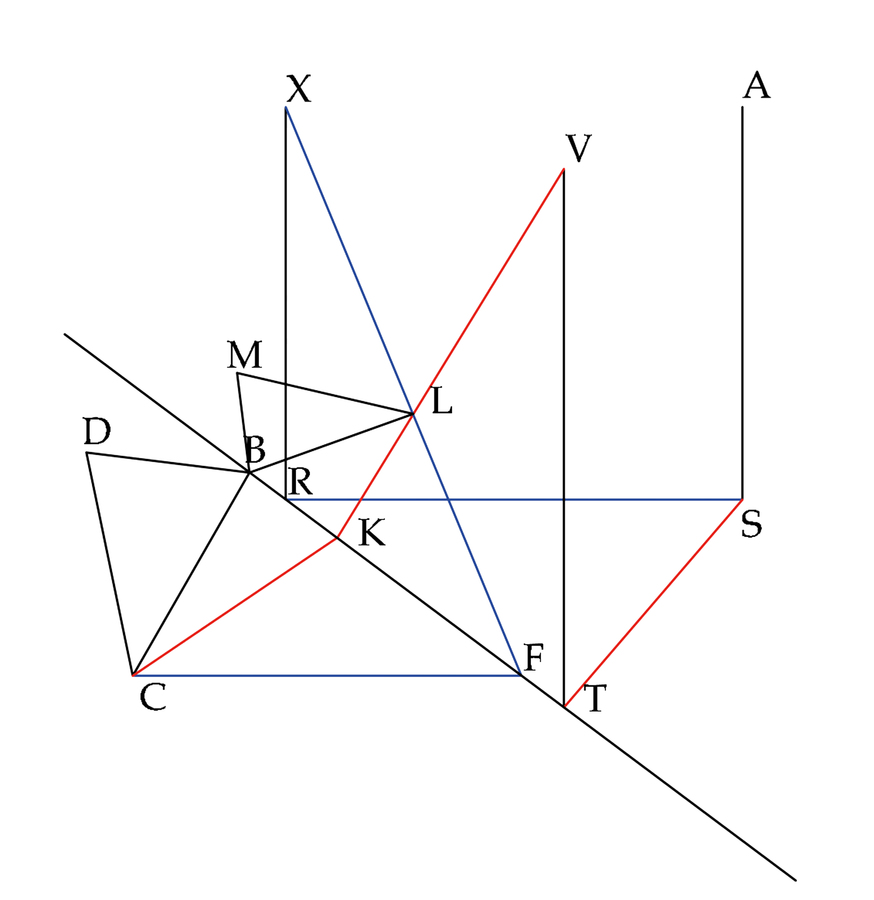
fig. 8.9: La successione delle fasi costruttive nel modo decimoquinto. Essendo i punti X al centro e V di fianco i punti di concorso rispettivamente delle rette CF e KC, il punto C, comune ad entrambe, appare in L, ove s’intersecano le prospettive delle rette date, concorrenti nei punti principale e di distanza.
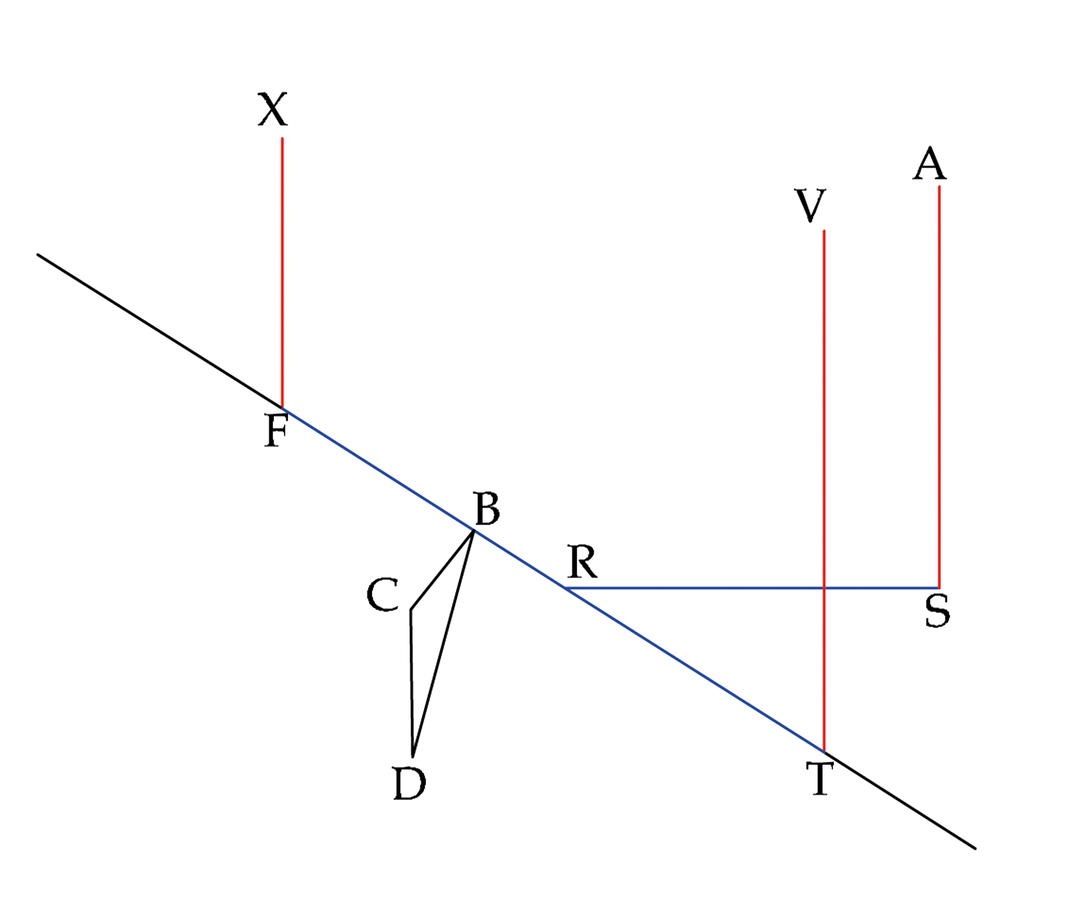
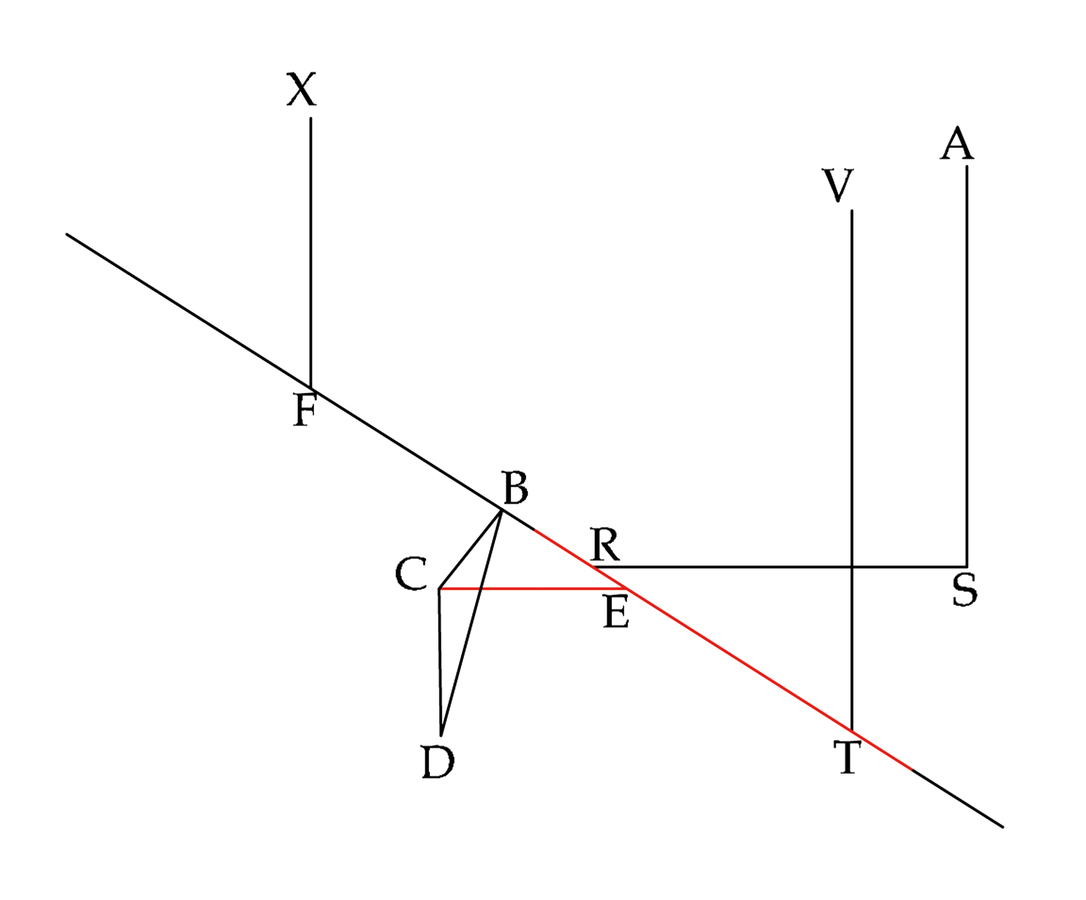
fig. 8.11: La successione delle fasi costruttive nel modo decimosesto. CE è perpendicolare a TF.
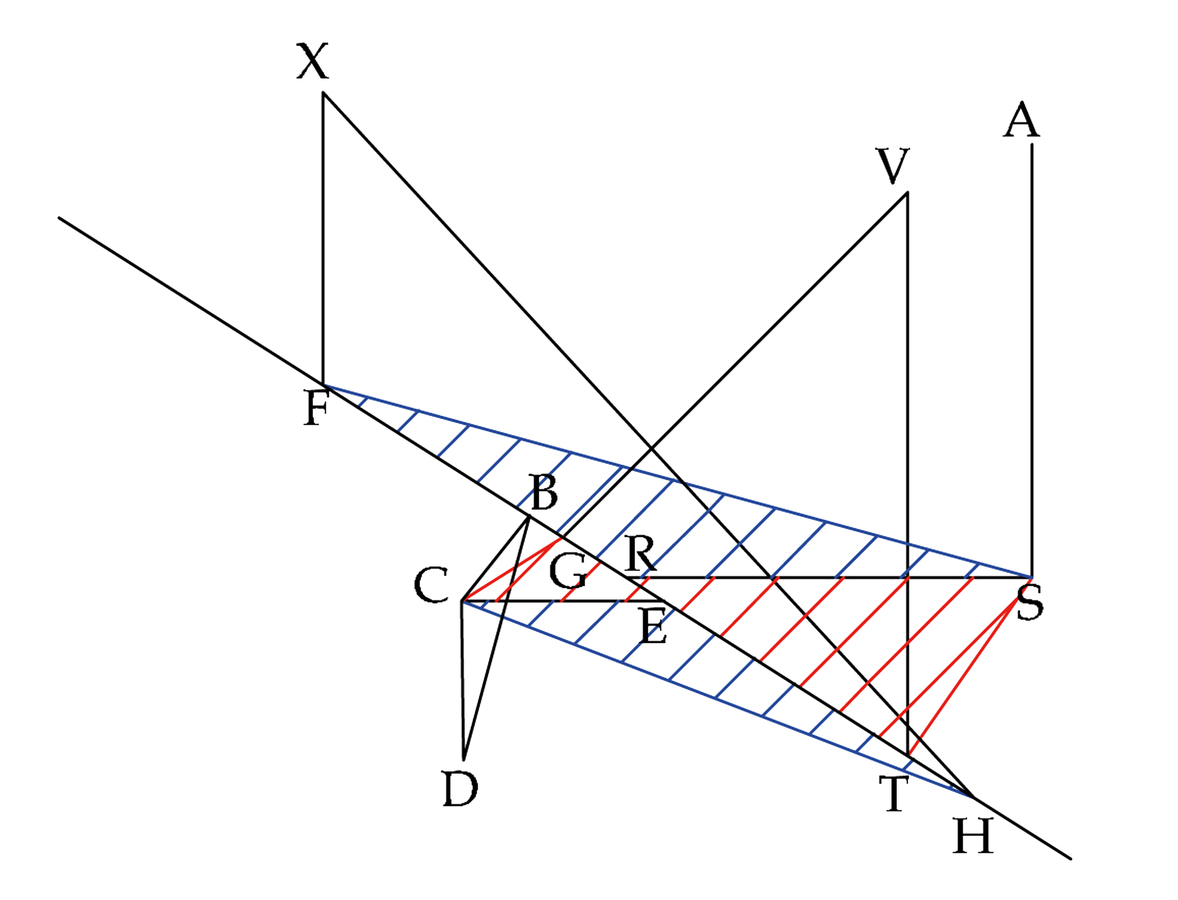
fig. 8.12: La successione delle fasi costruttive nel modo decimosesto. Si formano così quattro triangoli isosceli. Consegue che ST è parallela a CG e SF a HC.
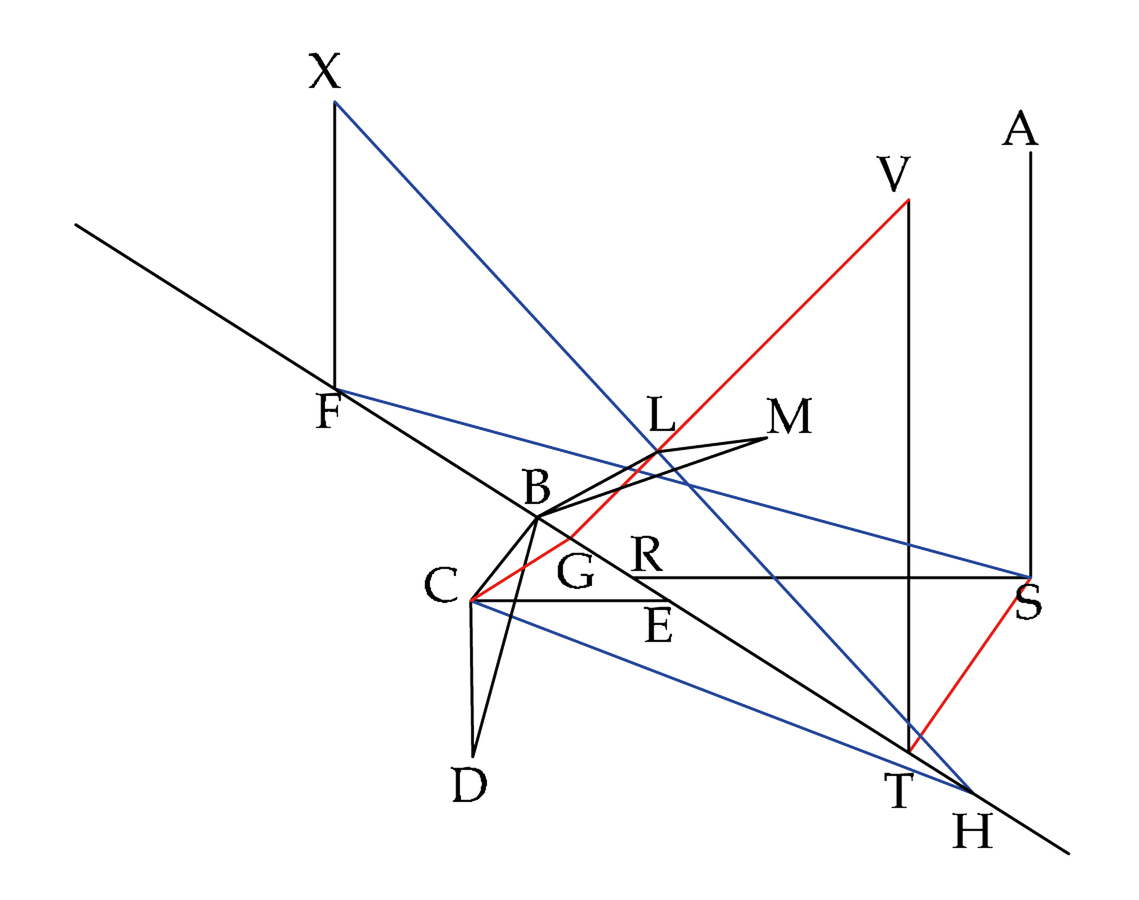
fig. 8.13: La successione delle fasi costruttive nel modo decimosesto. Essendo i punti V e X nel quadro i punti di concorso rispettivamente delle rette CG e HC, il punto C, comune ad entrambe, appare in L, ove s’intersecano le prospettive delle rette date, concorrenti nei due punti laterali.
Anziché a istanze incompatibili o a indirizzi in sé autonomi e persino reciprocamente alternativi, ci troviamo dinanzi a due delle tante possibili variazioni all’interno del medesimo sistema. Così come innumerabili possono essere le scelte stilistiche particolari e individuali dei singoli artisti.
4. Nel precedente convegno urbinate mi ero impegnato a indagare sulla formazione di alcuni concetti fondamentali dell’istituzione prospettica e sulla loro graduale evoluzione negli scritti teorici di Leon Battista Alberti
Quindi, l’artificio tecnico si fonda su due elementi reciprocamente funzionali e anche in correlazione allo sguardo di chi vede la prospettiva: il punto ove la perpendicolare dall’occhio incontra il quadro o che “il razzo centrico ferisce” (Alberti 1973, 20)
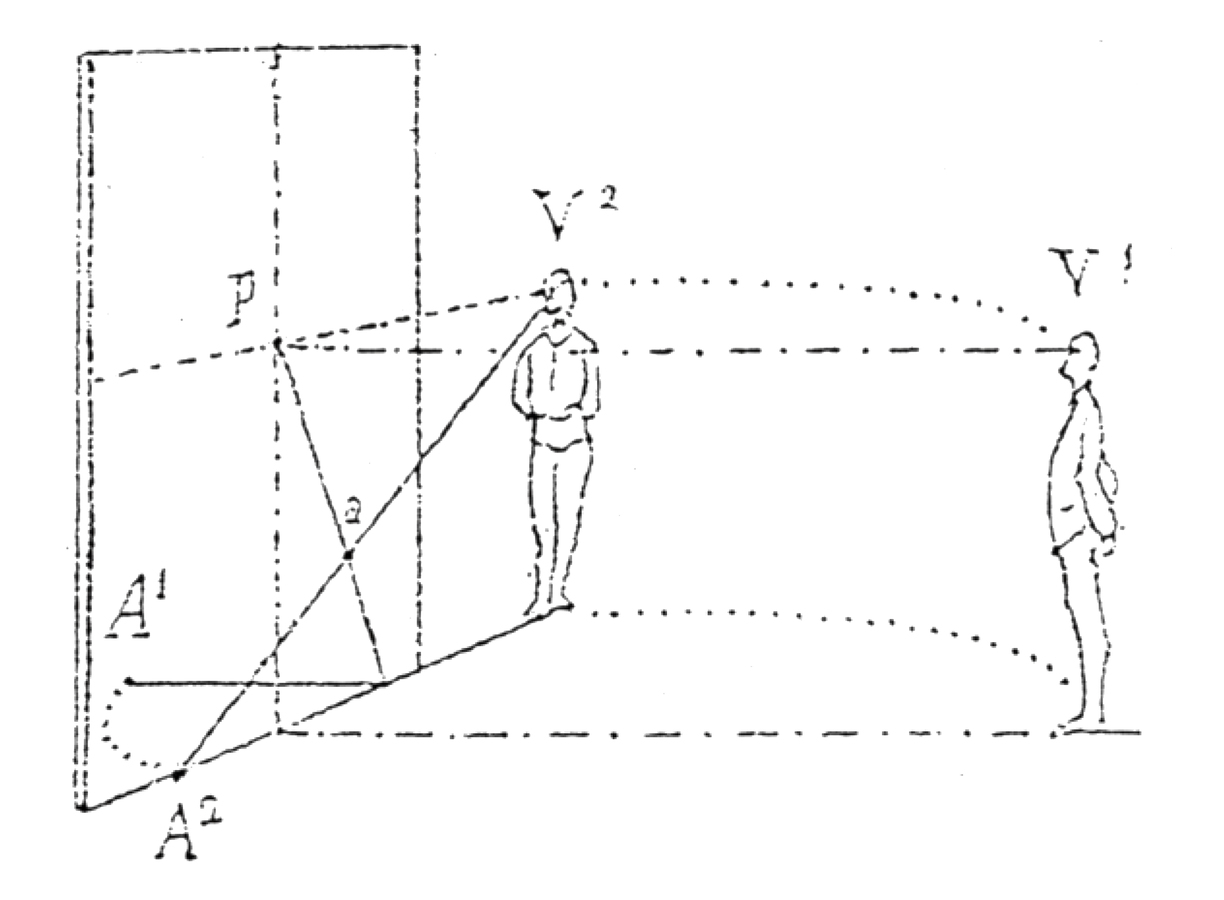
fig. 8.14: Alberto Maso Gilli, Ricostruzione del procedimento con punto di distanza.
Ora, con ammirevole sintesi e economia di passaggi grafici, Piero della Francesca
Immediatamente dopo la prima edizione del trattato De prospectiva pingendi nel 1899 (Piero 1899), si formò e si sviluppò nel tempo un’autorevole linea critica (Giulio Pittarelli, Giusta Nicco Fasola, Tullio Viola, Decio Gioseffi)
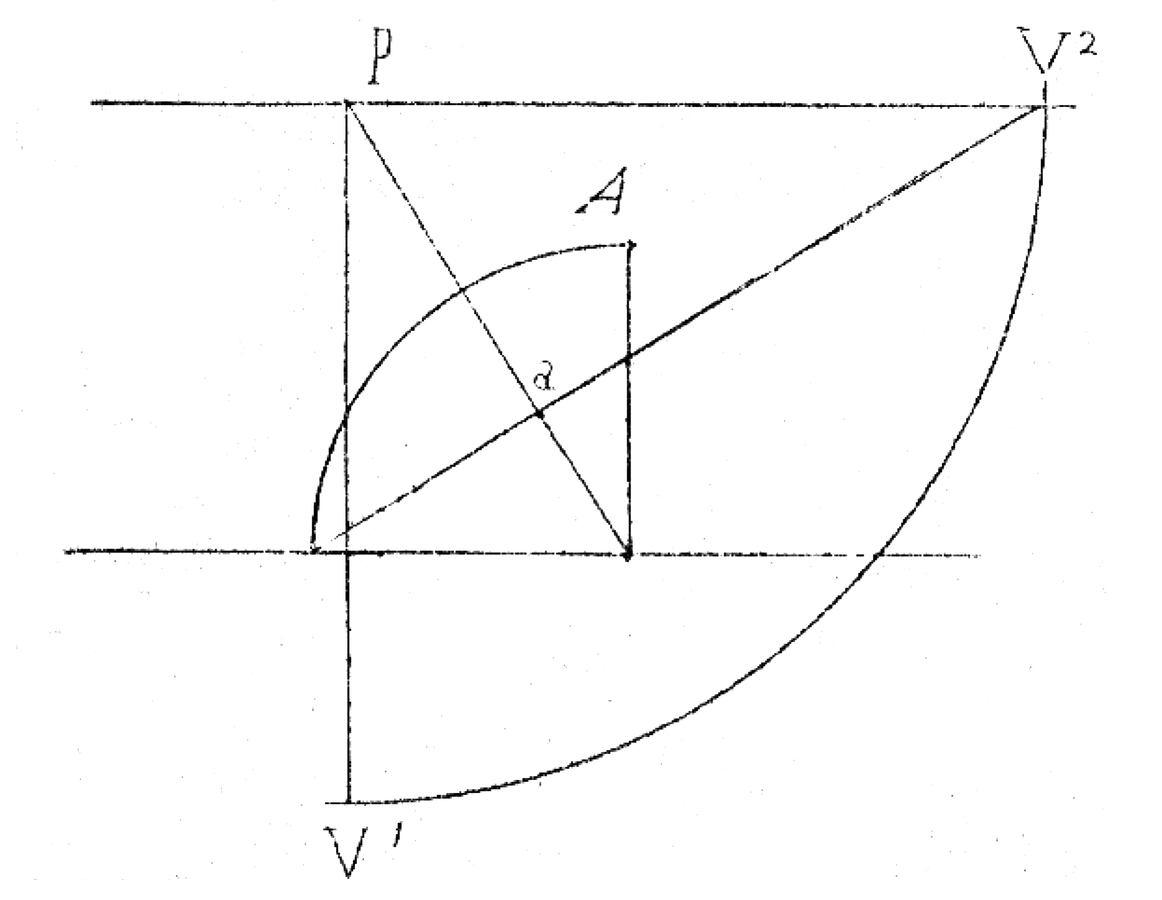
fig. 8.15: Alberto Maso Gilli, Dimostrazione geometrica del metodo con punto di distanza.
Giunsi a riconoscere l’esatta coordinazione degli elementi nelle varie fasi che scandiscono il procedimento in un disegno anche figurato e nella relativa dimostrazione geometrica (si vedano le due Figure 8.14 e 8.15), che in verità non si riferiscono specificamente al testo pierfrancescano, ma tuttavia lo implicano in modo decisivo (Figura 8.16).
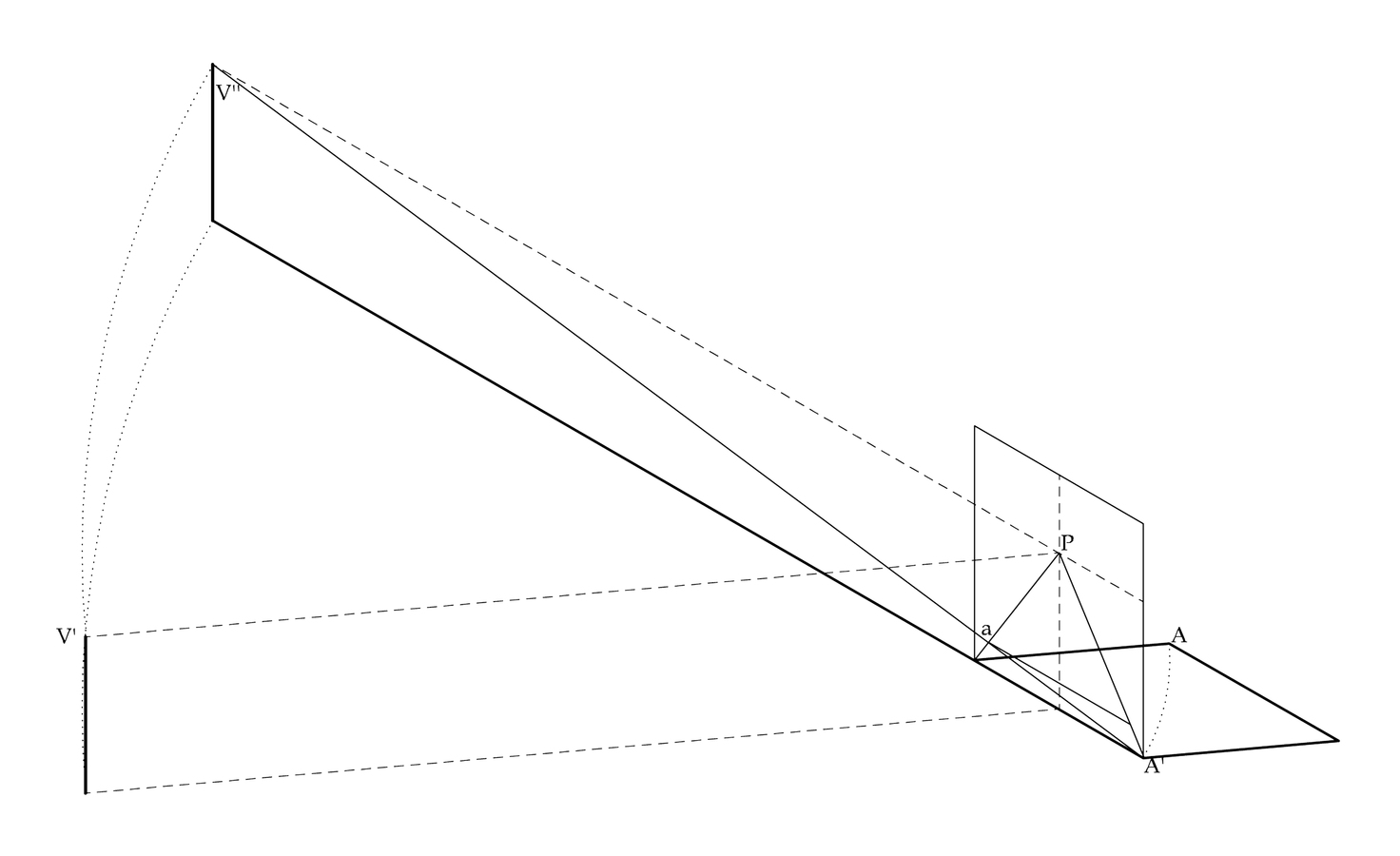
fig. 8.16: La correlazione degli elementi nel congegno prospettico pierfrancescano. Dalla proposizione XXIII del libro primo (disegno di Filippo Parroni).
Li ricavai da uno scritto che è un’autonoma e documentata riflessione rivolta proprio al significato e all’uso del termine “punto di distanza,” steso da un autore di diversa epoca, formazione e atmosfera culturale: il pittore e incisore piemontese Alberto Maso Gilli
Ritengo che non ci fosse da parte sua una predilezione del secondo gruppo sul primo, anche se al quadro mentale di un torinese e vicino ai Savoia s’imponeva l’influsso diretto della più recente scuola prospettica transalpina. È plausibile che il dominio di un così vasto svolgimento storico, che comportava il rapporto con la tradizione tanto rinascimentale italiana, quanto seicentesca francese, fosse per alcuni aspetti mediata attraverso la conoscenza approfondita della fondamentale Histoire de la perspective ancienne et moderne di Noël-Germinal Poudra
Nella pluralità di accostamenti e sullo sfondo dell’ascendenza prospettica francese manca appunto il riferimento diretto alle fondamentali proposizioni pierfrancescane. Nelle tavole sinottiche che corredano il saggio, infatti, Gilli
In compenso, diffusi sono i passaggi e numerose le esemplificazioni grafiche che tengono conto dei Perspectivae libri sex di Guidobaldo del Monte. Di fatto, non ho motivo di dubitare che il pittore Gilli
La stessa dimostrazione divenne il motivo ispiratore dello studio che egli dedicò al concetto di “punto della distanza.” In tale maniera, attraverso l’apporto del Poudra
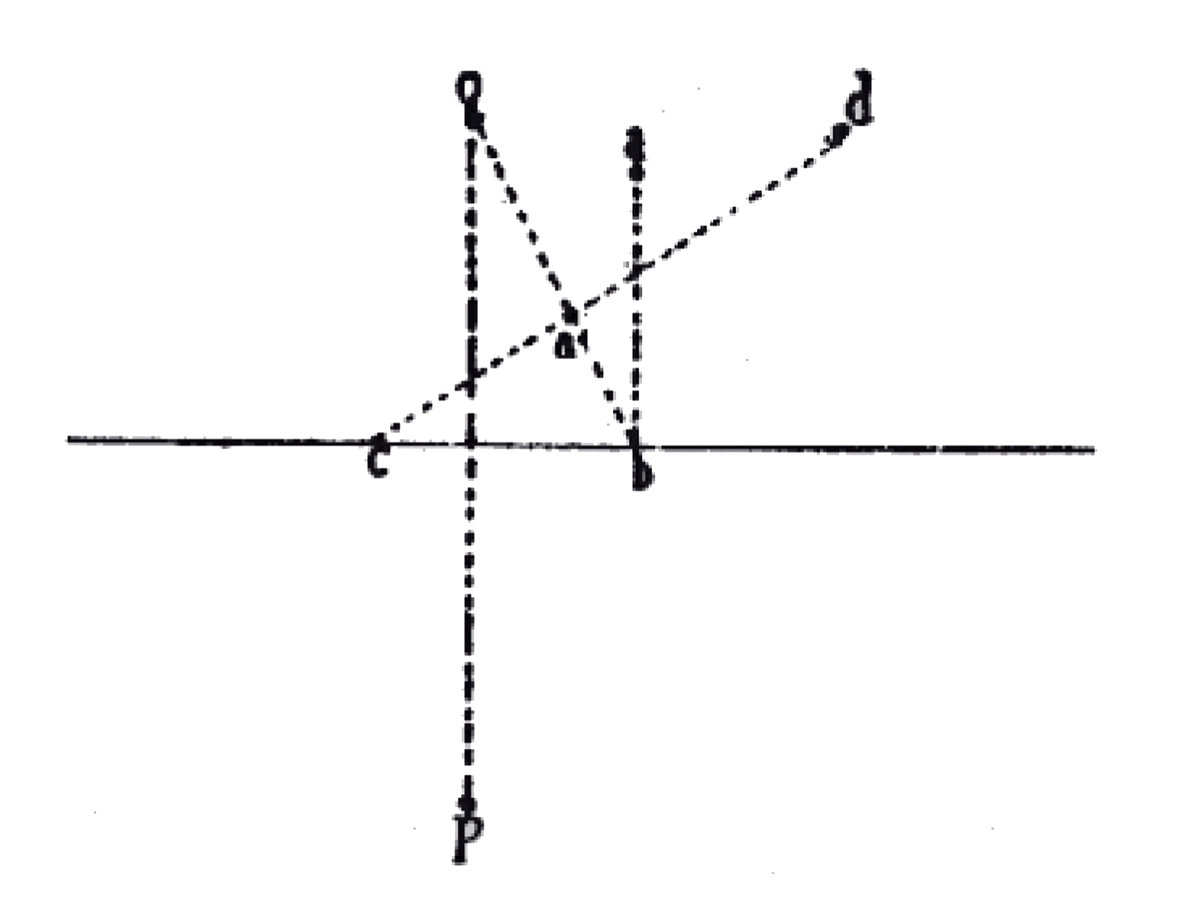
fig. 8.17: I. La distanza tra il punto p e il quadro sia trasportata dalla pianta sull’orizzonte di fianco al punto o (od). II. Dal punto dato a si conduca la perpendicolare alla linea di terra. III. Si prenda bc = ba. IV. Si congiunga c con d e b con o; l’intersezione delle due rette è la prospettiva del punto dato. Da Nöel-Germinal Poudra
Dall’altro canto, il fatto che la duplice presentazione grafica del medesimo assunto sia quella stessa di Guidobaldo pone Alberto Maso Gilli
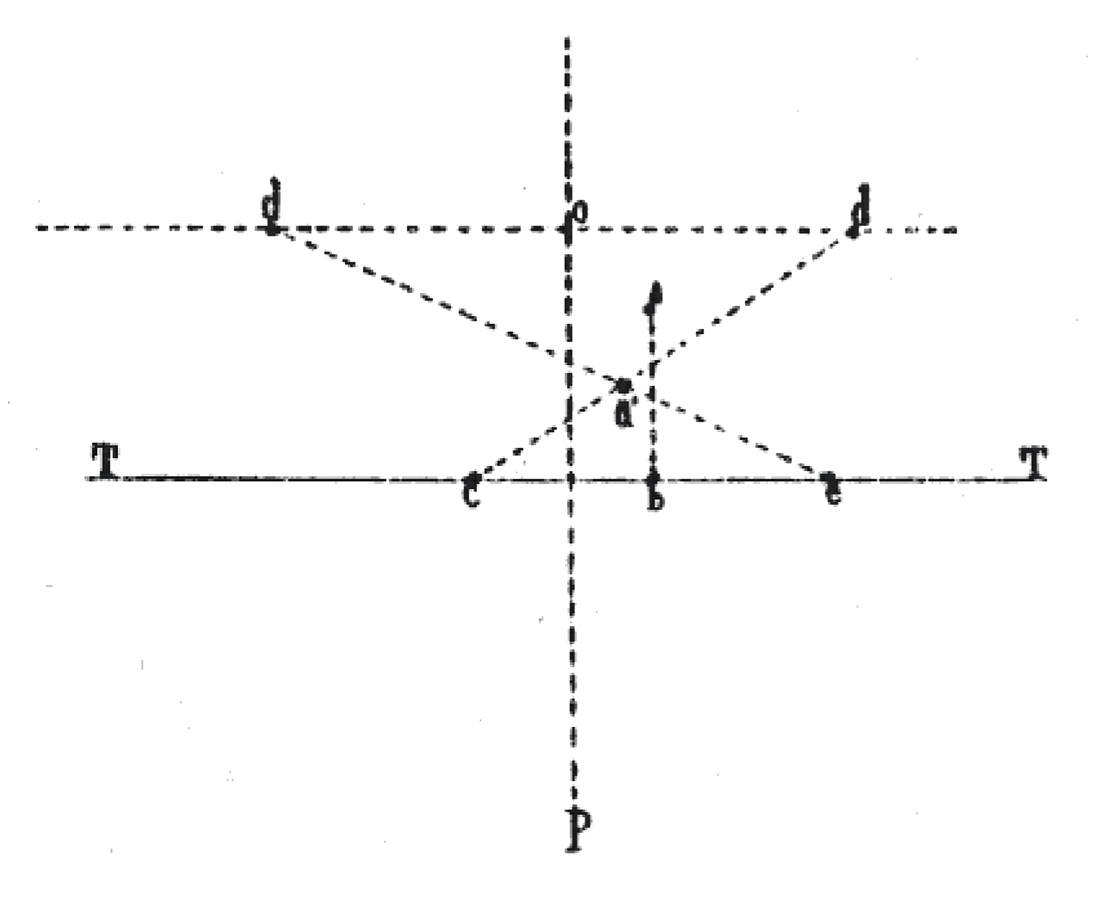
fig. 8.18: I. Siano i due segmenti od, a destra e a sinistra del punto principale, eguali alla distanza tra il punto p e la retta TT. II. Si abbassi dal punto dato a la perpendicolare alla retta TT. III. Alla sinistra e alla destra del punto b si fissino due punti in modo che bc = be = ab. IV. Si congiungano c ed e con i punti d; l’intersezione di queste due rette è l’immagine in prospettiva del punto dato. Da Nöel-Germinal Poudra
5. Nel secondo dei Perspectivae libri sex ciascun metodo operativo per rappresentare sul quadro la prospettiva di una figura piana è sempre espresso con due distinte formulazioni: la prima di carattere più astratto, a cui Poudra
La seconda formulazione attirò l’attenzione specifica degli studiosi e innanzitutto del Poudra
Indagando il processo costruttivo nella sua forma interna, egli ne abbreviò la successione delle fasi col mutare l’oggetto della prospettiva, che dalla figura triangolare divenne il singolo punto A (Figure 8.17 e 8.18).
Poté così tracciare un minor numero di linee e guadagnare in chiarezza col procedere ancor più concentrato e spedito. Quindi, la riduzione operata a partire dal testo geometrico diveniva interpretazione stessa dei suoi contenuti concettuali.
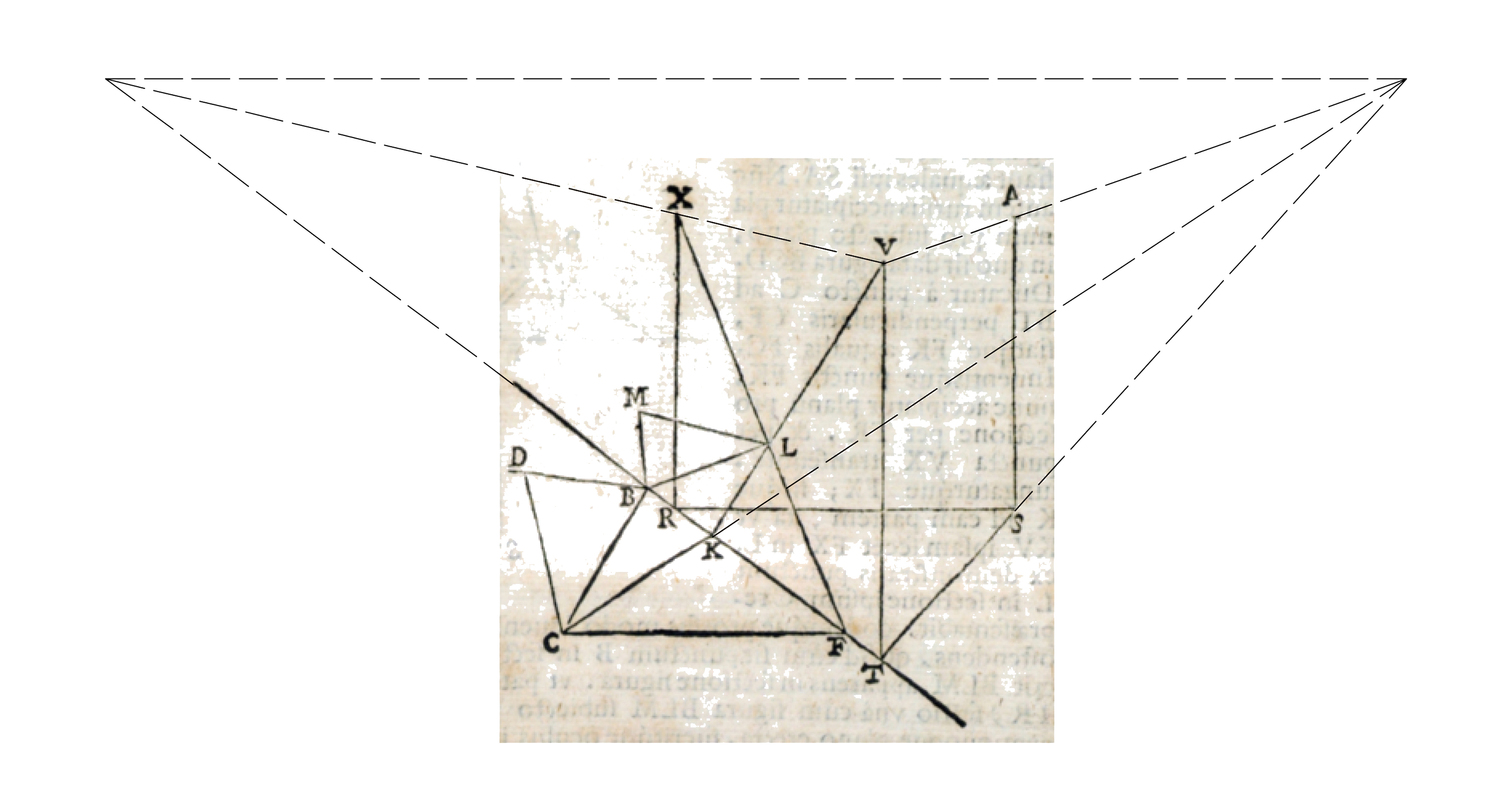
fig. 8.19: La dimostrazione di Guidobaldo è una veduta in prospettiva di una costruzione prospettica ripresa dall’alto, di lato e a distanza (schema grafico di Filippo Parroni).
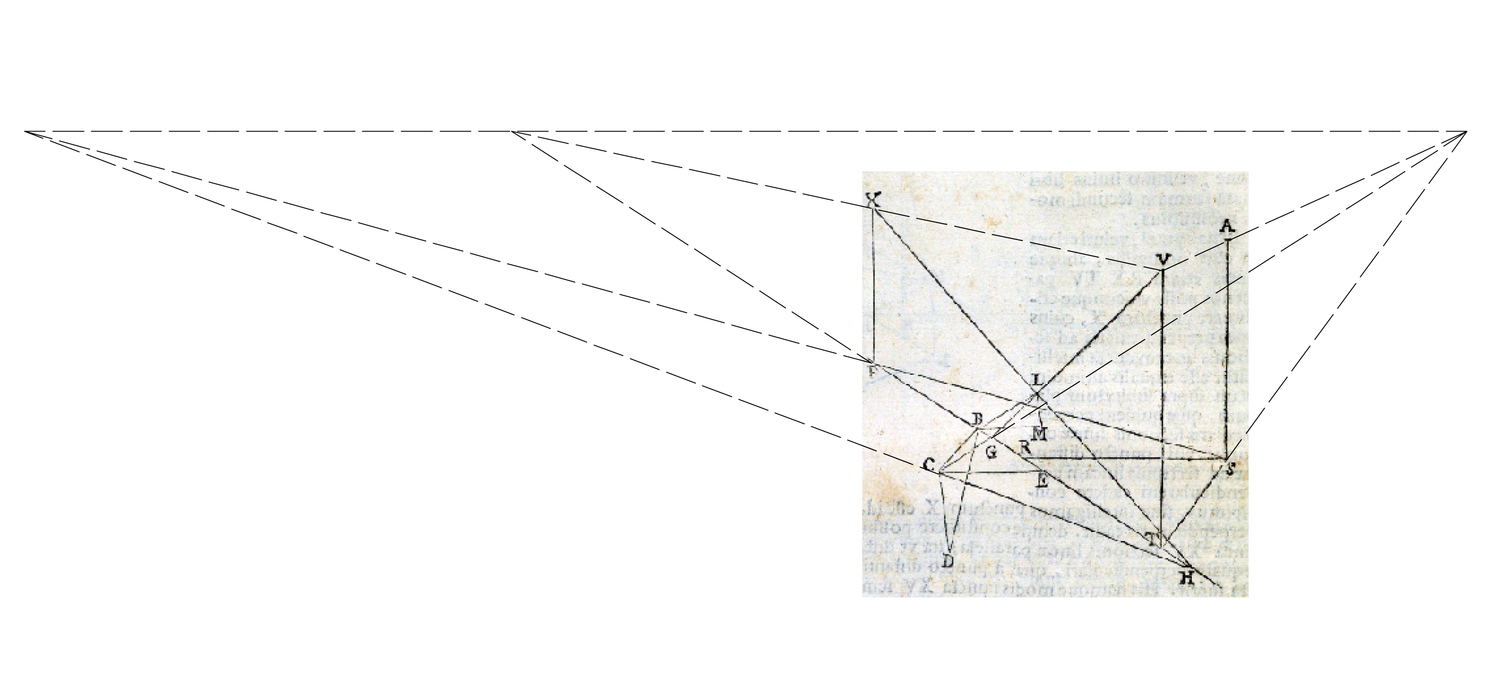
fig. 8.20: La dimostrazione di Guidobaldo è una veduta in prospettiva di una costruzione prospettica ripresa dall’alto, a distanza ravvicinata e secondo due punti accidentali (schema grafico di Filippo Parroni).
In sostanza l’artificio geometrico proposto da Guidobaldo si fonda sul ribaltamento del quadro sul piano orizzontale, assumendo come perno la linea di terra, così da presentare in vera e propria sovrapposizione sia la figura reale sia la figura apparente (Figure 8.3 e 8.5). L’una e l’altra sono gli estremi di un percorso visivo che la descrizione verbale e l’azione grafica seguono nella complessa serie di fasi e di movimenti successivi nel tempo. Nell’immagine la fissità ingenera il senso della temporalità e diviene dinamismo.
Per quanto mi consta, non sembra essere stata considerata davvero mai l’elaborazione teorica delle ventitré diverse modalità prospettiche. In ogni caso le costruzioni hanno notevole rilevanza teorica, nonché singolarità storica. Sono rappresentazioni in prospettiva del procedimento di costruzione prospettica (Figure 8.19 e 8.20), che mostrano forti analogie con il motivo dello spettacolo nello spettacolo nel teatro barocco.
La pittura, arte per eccellenza della rappresentazione visiva, osserva se stessa, si interroga sulla propria natura e indaga sul proprio funzionamento su basi rigorosamente geometriche. E la geometria sta alla pittura, come la retorica sta alla letteratura.
La tecnica della prospettiva costituisce una via d’accesso e al tempo stesso serve ad una verifica della meccanica dell’inganno visivo; è destinata in sostanza a svelarne retrospettivamente sia la natura illusoria, sia l’interno rigore strutturale.
In pittura, attraverso il congegno prospettico, l’imitazione si risolve nella propria perfezione ultima e assoluta ovvero nell’integrale coincidenza ottica con l’oggetto imitato. La finzione appare realtà, ma la nuova apparente verità, se si attua il disvelamento e la messa a nudo dell’ingranaggio che realizza la piena illusione, lascia ancora il posto alla finzione, si rivela subito come realtà fittizia.
Riferimenti
Alberti, L. B. (1973). De pictura. In: Opere volgari Bari: Laterza 7-107
Amodeo, F. (1932). Il primo sviluppo scientifico della prospettiva atrofizzò lo sviluppo della descrittiva. Atti dell'Accademia Pontaniana LXII: 105-149
Baytaz, N. (1644). Abbreviations des plus difficiles operations de perspective pratique. Annecy: par André Leyat.
Bourgoin, C. (1661). La perspective affranchie. Paris: chez Jollain.
Dalai Emiliani, M. (1968). La questione della prospettiva 1960-1968. L'Arte I: 96-105
Gilli, A. M. (1887). Difesa di una figura di prospettiva che si trova nel libro di Serlio L'Architettura. Dimostrazioni sul punto detto di distanza e raffronti prospettici. Roma: Ippolito Sciolla.
Gioseffi, D. (1957a). Complementi di prospettiva, 1. Critica d'arte 24: 468-488
- (1957b). Perspectiva artificialis. Per la storia della prospettiva, spigolature e appunti. Trieste: Tip. Smolars.
- (1994). Scritti di decio Gioseffi sulla prospettiva. Arte in Friuli-Arte a Trieste
Libri, G. (1838-1841). Histoire des sciences mathématiques en Italie depuis la renaissance des lettres jusqu'à la fin du dix-septième siècle. Paris: Renouard.
Longhi, R. (1914). Piero dei Franceschi e lo sviluppo della pittura veneziana. L'Arte
- (1961). Opere complete di Roberto Longhi. Firenze: Sansoni.
Maltese, C. (1974). Architettura “ficta” 1472 circa. In: Studi bramanteschi Roma: De Luca 283-292
Marconi, S. (2009). Anatomia di due disegni pierfrancescani. In: L'arte della matematica nella prospettiva, Atti del Convegno Internazionale di Studi (Roma-Urbino, 8-11 ottobre 2006) Foligno: C.B. Cartei & Bianchi 313-323
Monte, Guidobaldo del (1600). Perspectivae libri sex. Pesaro: Girolamo Concordia.
Moreno, P. (1987). Pittura greca. Da Polignoto ad Apelle. Milano: Arnoldo Mondadori.
Panofsky, E. (1927). Die Perspektive als 'symbolische Form'. In: Vorträge der Bibliothek Warburg 1924-1925 Ed. by F. Saxl. Leipzig-Berlin: B.G. Teubner 258-330
Piero, della Francesca (1899). Petrus Pictor Burgensis. De prospectiva pingendi. Strassburg: Heitz.
- (1942). De prospectiva pingendi. Firenze: Sansoni.
Poudra, N. G. (1864). Histoire de la perspective ancienne et moderne. Paris: J. Corréard.
Sinisgalli, R. (1984). I sei libri della prospettiva di Guidobaldo dei marchesi Del Monte dal latino tradotti, interpretati e commentati da Rocco Sinisgalli. Roma: L'Erma di Bretschneider.
Vignola, J. Barozzi (1583). Le due regole della prospettiva pratica di M. Iacomo Barozzi da Vignola, con i comentarij del R.P.M. Egnatio Danti dell'ordine de predicatori, matematico dello studio di Bologna. Roma: Francesco Zannetti.
Note a piè pagina
Cfr. (Alberti 1973, 92–93). Il riferimento al pittore Panfilo è desunto da Plinio.
Quintiliano, Institutio oratoria, X, 2, 7.
Plinio il Vecchio, Naturalis historia, XXXV, 15.
Atenagora, Πρεσβεία περὶ τῶν Χριστιανῶν, 17.
Per l’analisi critica delle fonti su Apollodoro e per il raccordo con gli sviluppi figurativi nel Quattrocento italiano si veda (Gioseffi 1957a, 478–480), ora in (Gioseffi 1994, 175–180).
Si vedano in particolare le voci σκιά, σκιαγράφος nel Λεξικόν di Esichio Alessandrino.
Plinio, op. cit., XXXV, 60.
Vitruvio, De architectura, VII, praef., 11.
Sul ruolo di Apollodoro nello svolgimento della storia pittorica si veda anche (Moreno 1987, 81–83).
La nota definizione longhiana appare per la prima volta nel fondamentale saggio: Piero dei Franceschi e lo sviluppo della pittura veneziana (Longhi 1914), ora in (Longhi 1961, 66).
Federico Amodeo osservava che “Guido Ubaldo del Monte ha il gran merito di aver generalizzata la
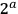 regola di Vignola a due qualunque punti della linea d’orizzonte” (Amodeo 1932, 149).
regola di Vignola a due qualunque punti della linea d’orizzonte” (Amodeo 1932, 149).
Pur con sfumature diverse seguono la stessa impostazione critica gli studi di John White, Alessandro Parronchi, Robert Klein, Liliane Brion-Guerry. Si veda il resoconto di Marisa Dalai Emiliani (Dalai Emiliani 1968).
Cfr. (Gioseffi 1957b, 87; ora in Gioseffi 1994, 101–102).
