4.1 Zerbrechliche Teleskope
Der Unterschied zwischen beiden Wissensfeldern ist dennoch bemerkenswert: Während für die Architektur das Werk
4.2 Mechanica und machinatio
Auf der Basis eines kenntnisreichen saper fare (Wissens, wie etwas zu machen ist) entstanden tatsächlich einige der bemerkenswertesten, gerade in statisch-konstruktiver Hinsicht interessanten Bauwerke der Renaissance. Dazu gehört der (Wiederauf-)Bau der Ponte Santa Trinita in
„Was also das Abrutschen von besagter Mauer angeht, ist dies meines Erachtens unmöglich, wenn man das Beispiel der ungleicharmigen Waage heranzieht […] wenn wir in diesem Beispiel den Palazzo mit der ungleicharmigen Waage gleichsetzen, erkennen wir in ihm dieselben Elemente, die wir bei ihr benannt haben, als da wären folgende: Gehen wir zunächst davon aus, dass der Haken an der Stelle des Balkones des Versammlungssaales des gran Consiglio anzusetzen wäre […].“6
Die Biografie des „inzegnero“
Andere Autoren, denen man wertvolle Schriften zur Architektur verdankt, bieten keine weitergehenden Hinweise – ihre Überlegungen zu Stabilität und Festigkeit gehen üblicherweise nicht über das Stadium einfacher Andeutungen hinaus. Wo dies der Fall ist, wie bei den von
Zu diesem historischen Problem gesellt sich ein historiografisches. Die Quellen, die es erlauben würden, einen überzeugenden Bezug zwischen mechanischen Kenntnissen und architektonischen Konstruktionen herzustellen, sind größtenteils noch nicht hinreichend untersucht, in vielen Fällen vielleicht sogar erst noch zu entdecken bzw. wiederzuentdecken. Gelten für die spätere Zeit die Discorsi e dimostrazioni matematiche (1638)
Tatsächlich jedoch sagt die Abhandlung über die Gestalt der Hölle vergleichsweise wenig über die resistentia solidorum und die Strukturmechanik aus. Was
„Aber lassen wir die Architektur beiseite und schauen wir, ob diese Konstruktion stabil bleibt, wobei wir meines Erachtens feststellen werden, dass dies nicht der Fall sein kann. Denn angenommen, dass der Höllenschlund mit gleich weit voneinander entfernten Rändern aufsteigt, so ruhen die oberen Partien nicht auf einem haltenden Fundament und werden daher zweifellos einbrechen. Denn da schwere Körper beim Fallen eine Strecke beschreiben, welche sie direkt zum Erdmittelpunkt führt, brechen sie ein und fallen, sofern sie auf dieser Strecke nicht auf etwas stoßen, das sie aufhält und stützt, […]. Wenn über diesem Nichts die anderen Steine konvergieren und sich stützen, dürfen sich die Mauern, welche sie tragen müssen, nicht außerhalb der senkrechten Linie befinden, die zum Erdmittelpunkt führt. Dieser Nachteil wird inManettis Architektur nicht erwähnt.“11
Im Folgenden widmet sich
„Hier könnte man uns entgegenhalten, dass man nicht einmal die Hölle für so groß halten darf wie es beiManetti der Fall ist. Denn, wie Einige vermutet haben, scheint es unmöglich, dass das Deckengewölbe der Hölle halten könne ohne einzustürzen und in ebendieser Hölle zu versinken, wenn es so dünn wäre wie es sein müsste, wenn sich die Hölle derart hoch erstreckt. Es wäre nicht dicker als der achte Teil des Erdradius, also etwa 405 Meilen, und es käme hinzu, dass man davon noch den Platz für die Grotte der Unglückseligen wie auch für die erhebliche Distanz zwischen Meeresoberfläche und Meeresboden abziehen müsse. Dem kann man leicht antworten, dass diese Dicke voll und ganz ausreicht; denn nimmt man ein baugleiches kleines Gewölbe mit einem Bogen von 30 Ellen, bleiben etwa vier Ellen für seine Dicke. Das ist mehr als genügend, denn selbst wenn man für seine Dicke bei einem Bogen von 30 Ellen nur eine einzige Elle (anstelle von vieren) vorsieht, vielleicht auch nur eine halbe, wird auch das ausreichend stabil sein. Da wir nun wissen, dass die Meere wenige Meilen, ja sogar weniger als eine einzige Meile tief sind, wenn wir den erfahrensten Seeleuten Glauben schenken, können wir die Zahl der Meilen bestimmen, die uns für die Grotte der Unglückseligen erforderlich scheinen, da uns der Dichter kein genaues Maß angegeben hat. Wenn wir nun noch annehmen, dass zwischen dieser und dem Meeresboden 100 Meilen liegen, wird das Gewölbe nichtsdestotrotz sehr dick bleiben und sogar dicker sein als es nötig wäre, um zu halten.“12
Einige Forscher haben diesen Seiten des Frühwerks besondere Bedeutung zuzuschreiben gesucht.13 Doch der Verdienst von
So sind die Bemerkungen
„[…] ich muss zugeben, dass es mir nicht gelungen ist, meinen Ansatz mit der Deutlichkeit zu erläutern, die erforderlich ist, um sich gut zu verständlich zu machen, insbesondere wenn man Vorschläge vertritt, die nicht den allgemeinen Auffassungen entsprechen. Ich muss daher feststellen, dass meine Intention eine ganz andere, dem Verständnis von Euer Wohlgeboren sogar völlig entgegen gesetzte war.“16
Schon vorher hatten andere Autoren zu diesem Thema vereinzelte Anregungen angeboten, die den Weg zu einer Lösung hätten erleichtern können, jedoch erst im frühen 17. Jahrhundert gebündelt werden und Früchte tragen sollten. Klassische Bezugspunkte, die eine Untersuchung lohnten und sich als entscheidend für die moderne Formulierung von Problemen der Strukturmechanik erweisen sollten, waren die im Verlauf der Renaissance intensiv studierten und kommentierten Werke von fünf Autoren:
Von diesen Autoren und ihren Werken gingen auch die Untersuchungen Guidobaldo del
Die berühmte, von Domenico
Dieser kurze Discorso ist an den Grafen von
„ein Magazin von Militärmaschinen und solchen zum Bewegen von Lasten eingerichtet, von denen er etwa ein Dutzend verschiedene eigenhändig hergestellt hatte, teils zum Ziehen, teils zum Heben außergewöhnlicher Lasten mit äußerst geringer Kraft.“21
Ein „Speicher“ (magazino) besonderer Art, der auch „Treffpunkt verdienter Personen und Heimstatt von Soldaten und Gelehrten“22 war: ganz im Einklang mit der Idee eines stanza dell’architettura militare (der Festungsarchitektur gewidmeten Kabinetts), mit der sich
Im Umfeld des Transportes des Vatikanischen Obelisken sind demnach einige der herausragenden Köpfe dieser Zeit zu erkennen. Der Ort des Geschehens, wenige Jahre vor der Baustelle der Kuppel des Petersdomes und unweit von dieser eingerichtet, war scheinbar ein ideales Experimentierfeld für diejenigen, die sich mit den Prinzipien der neuen Wissenschaft der Mechanik befassten. Auf der von Domenico
Die als Bezugspunkt herangezogenen antiken Quellen entstammten der Welt der Mechanik und der Architektur, wie das von
4.3 Über die Mechanischen Probleme hinaus
Wie schon erwähnt gilt traditionell das Erscheinungsdatum der Discorsi e dimostrazioni matematiche intorno a due nuove scienze (1638) von Galileo
Diese Interpretation beruht auf einem problematischen Verständnis der Geschichte der
Das statische Wissen der Baumeister der mittelalterlichen Kathedralen ist so im Detail ebenso unbekannt wie die Kenntnisse, auf deren Basis Filippo
Das 16. Jahrhundert interpretierte den Baukörper häufig als in seiner Stabilität bedrohte „Maschine“. Damit wurde an theoretische Überlegungen der griechischen Mechanik angeknüpft, ein weiterer obligatorischer Bezugspunkt war das Buch X der De Architectura von
Dieselben Themen beschäftigten Bernardino
Während
Die minutiöse Auseinandersetzung mit den 35 Problemen (die
„Monsig.r, der Abt vonGuastalla hat mich wissen lassen, dass er, wenn man nun die Ponte del Baccanello erneuern muss, einen wunderschönen Entwurf für eine Brücke hat, den er gerne umsetzen würde, und er wünscht von Euer Wohlgeboren gehört zu werden und wenn er mit Ihnen gesprochen haben wird, oder Ihnen schriftlich das Nötige mitgeteilt hat, wird er Ihnen das Modell davon zeigen.“34
In theoretisch-literarischer Hinsicht bezeugen zwei Hauptwerke
„Als AdrianoRomano aus Polen zurückkehrte, wo er einem Mitglied des Hofes Vitruv erläutert hatte, sagte er manchmal, dass er, wenn er in Polen den Kommentar Baldis zur Verfügung gehabt hätte, er diesen sozusagen um seinen Lohn gebracht hätte, weil er selbst seine Aufgabe dann völlig mühelos hätte erledigen können.“37
Das zweite ist ein Meisterwerk der Beschreibungskunst, wie Giovan Mario
„[…] und obgleich er sich damals weit von dieser Stadt entfernt befand, verfasste er es nichtsdestotrotz mit der Hilfe sowohl des Planes, den er selbst vorher verfertigt hatte, als auch seiner wunderbaren Erinnerungskraft, mit solcher Genauigkeit, wie er es gemacht hätte, wenn er sich inUrbino befunden hätte: eine Fähigkeit, die in der Profession des Architekten als sehr nützlich gilt, denn da die Örtlichkeit dieses Palastes recht schwierig ist, gelingt es nur mit Mühe, aus dem einfachen Plan seine innere Schönheit zu erkennen.“38
Die technischen Charakteristika dieses Palast-Universums werden von den Fundamenten bis zu den Dächern peinlich genau beschrieben. Dabei wird auf die Eigenschaften der Materialien eingegangen, auf die geistreichen konzeptionellen Lösungen und auf die Einsichten, mittels derer es gelungen war, „eine so große Maschine“ (una macchina così grande) prachtvoll und harmonisch zu gestalten, indem materia e forma gekonnt vereint wurden.39 Im Kommentar zum sechzehnten der Mechanischen Probleme widmet sich
Das Studium von Texten zur Mechanik und Texten zur Architektur verlief also bei
„Warumb under 2 Hölzern gleicher grösse ans Knie gehalten / das jenige leichter zerbrochen werde / so mit beyden Händen zu allereusserst als das so nahe beym Knie gefasset worden: Und wiederumb so man mit dem Fuß auff ein Holz tritt / nachmalen dasselb an beiden eussersten enden erwischt und kräfftiglich beuget / solchs eher und leichter entzwey gehe / als wann mans gar nahe bey dem Fuß gefasset und angedähnet hette?“41
Im Sechzehnten ist die Frage tückischer:
„Woher es komme / daß je länger die Höltzer / je schwächer sie werden / und sich im auffheben biegen; Ein kleines (zum Exempel 2 Elen langes) doch dünn und schwanckes / eben so wol / als ein dick grob und starckes so 100 Elen lang?“42
Die Überlegung
Man darf nicht vergessen, dass dieser Perspektivwechsel für die im Entstehen begriffene ‚rational mechanics‘ ein dauerhaftes Ärgernis darstellen wird. Pierre-Simon
„Wenn es in der Theorie der Statik erlaubt ist, Hebel als Mittel zu sehen, durch die bewegte Körper aufeinander wirken als wären sie völlig starr, so ist diese Annahme bei der Anwendung dieser Wissenschaft auf die Berechnung von Maschinen nicht mehr anwendbar, denn die Natur hat keinen Stoff geschaffen, dessen Bestandteile nicht durch die Anwendung einer bestimmten Kraft voneinander getrennt werden könnten. Es gibt also zwei Arten von Gleichgewicht, die beim Hebel und den von ihm abgeleiteten Maschinen bedacht werden müssen: die eine besteht zwischen entgegengesetzten Kräften, die sich ausbalancieren, die andere zwischen einer bestimmten Funktion dieser Kräfte und dem Zusammenhalt der Teile, aus denen die Maschinen zusammengesetzt sind. Die Bedingungen der ersten Art kann man eindeutig bestimmen, die der zweiten jedoch nur annähernd.“43
In allgemeinerer Form handelt es sich um ein Problem, das die epistemische Differenz zwischen Grundgleichungen des Gleichgewichtes und Zustandsgleichungen verkörpert. Noch im 19. Jahrhundert hatte die Elastizitätstheorie als direkter Erbe dieser Überlegungen aufgrund genau dieser subtilen Unterschiede Schwierigkeiten sich durchzusetzen. Dies zeigt sich an den von Louis
„Um die festen Körper mathematisch zu behandeln, ist es seiner Meinung nach notwendig, dass man akzeptiert, sie mathematisch zu definieren. ‚Mein Spazierstock‘, sagte er oft, ‚ist kein fester Körper. Er kann nicht nur brechen, sondern, was hundertmal schlimmer ist, er ist auch biegsam‘.“44
Die von
Für
„Um nun aus diesem Studium – das ansonsten unnütz scheinen könnte – irgendeinen Nutzen zu ziehen, und damit unsere Argumente helfen, die Architekten vorsichtiger zu machen, werden wir passenderweise unsere Überlegungen auf die Architektur anwenden.“46
Unter dieser Prämisse geht
„Ich glaube nämlich, daß die Menschen auf folgende Weise dazu geführt werden, einen Bogen zu spannen. Als sie sahen, daß man zwei Balken mit verbundenen Kopfenden unten mit auseinandergespreizten Füßen, so befestigen könne, daß sie in wechselseitiger Neigung und gleichem Gewichte gegeneinander stehenbleiben, gefiel ihnen diese Erfindung, und sie begannen auf diese Weise den Gebäuden zweitraufige Dächer aufzusetzen. Als sie hierauf, wie sie beabsichtigten, eine größere Fläche infolge der Kürze der Balken nicht überdecken konnten, setzten sie an den oberen Enden der Stämme ein Zwischenglied ein, so daß es fast die Form wie der griechische Buchstabe (Π) annahm. Diesen Zusatz nannten sie vielleicht Keil. Indem sie sodann dieses Verfahren fortsetzten, und durch Vervielfältigung der Keile auf diese Weise das Bild eines Bogens erblickten, gefiel ihnen dies und sie übertrugen diese Weise, einen Bogen zu bilden, auf das Steinmauerwerk und machten durch weiteres Hinzufügen von Keilen einen ganzen Bogen […].“47
Die elegante historisch-genetische Rekonstruktion wird zu einem erhellenden Hinweis auf die Mechanik und konnte als solcher der Aufmerksamkeit des Abtes von
Die Originalität der Exercitationes wirft die Frage auf, ob sich Quellen identifizieren lassen, auf die
Ein weiteres bedeutendes historiografisches Problem betrifft die Frage, ob oder inwieweit
Trotz dieser Verbreitung des Werkes auf europäischer Ebene wird
4.4 Von Urbino nach London, über Venedig
Dieselbe Quaestio XVI der Mechanischen Probleme dient dem englischen Gelehrten Henry
„Wenn Bausteine der üblichen rechteckigen Form einer neben dem anderen waagrecht zwischen Stützen gelegt werden, welche die Enden dieser Lage halten, dann werden zwangsläufig alle Steine zwischen diesen Stützen herunterfallen, schon allein durch die ihnen eigene natürliche Schwere. Dies gilt umso mehr, wenn sie eine Belastung durch ein zusätzlich auf ihnen lastendes Gewicht aushalten müssen. Denn weil ihre Seiten parallel zueinander ausgerichtet sind, haben sie, dem vorangehenden Theorem entsprechend, genügend Raum, ungehindert senkrecht fallen zu können. Damit sie also halten, müssen wir entweder ihre Lage ändern, oder ihre Form, oder beides.“54
In Bezug auf die „naturwissenschaftlichen“ Interessen von
„[...] 29. Die Automati von Heron vonAlexandria, in 4°. 30. Die Spiritali von ebendiesem, mit Illustrationen, in 4°. 31. Die Prospettiva von Euklid, kommentiert von Ignatio Danti, in 4°. 32. Die Geographia von Maurolico, in 4°. [...] 36. Eine Abhandlung, in 4°, von Galileo über die schwimmenden Körper.“55
Diese Daten sind sicher für
Es stellt sich die Frage, ob er nicht englische Vorbilder in diesem Feld hatte, an denen er sich hätte anlehnen können. Es deutet hier vieles auf ein bestimmtes Werk, einen kurzen Essay, der in
Der Praeface ist als eine wichtige Etappe zwischen dem mittelmässigen The First and Chief Groundes of Architecture von John
Die Spuren des Einflusses von
1 Der Titel, damals gar nicht gängig für ein architektonisches Werk: Elements, Elementa (Elements of Geometry/Elements of Architecture).
2 Die Verwendung der Wörter ,Theorem‘ und ,Korollar‘ in Verbindung mit der Gewölbetheorie: Auch diese Termini waren ohne Beispiel in der architektonischen Fachliteratur. Sogar
3 Die Zahl fünf: fünf Theoreme, fünf Postulate von
4 ,Mathematik‘, ,Mechanik‘, ,Natur‘. Weiter können wir feststellen, dass
Die Verwendung von Begriffen wie ,naturall‘, ,mathematicall‘, ,mechanicall‘, ,logicall‘ und so weiter würde eine separate Betrachtung verdienen. Hier sei nur angemerkt, dass in den semantischen Abweichungen dieser Begriffe ein Echo der Debatte wiederzufinden ist, die in der frühen Renaissance Ingenieure, Architekten und Mechaniker angefeuert hatte und die ein wichtiges Diskussionsthema zwischen
Weder
„Ich habe gehört, dassWotton sich nun in irgendeine Ecke des Landes zurückgezogen hat, um ein angefangenes Werk zu den mathematischen Wissenschaften, oder vielleicht auch zum Bauen von Luftschlössern, zu vollenden.“65
Vielleicht haben die Architekten (und die Historiographen) deswegen bis jetzt beide vernachlässigt.66 Vielleicht war
Die Schriften
Für Bernardino
„Die Masse der praktischen Architekten wird mich anklagen, wenn ich anstelle von ihnen überVitruv und Leon Battista schreiben werde. Doch diese, geschmückt, wie man sagt, mit allen Waffen, haben das Kampfrecht im Heer der Mathematiker, deren Biografien ich schreiben werde. Dasselbe sage ich den nur praktisch arbeitenden Mechanikern, auch wenn sie mittels der einfachen Praxis Wunder bewirkt haben.“68
4.5 Die science des architectes
In der Royal Society waren Robert
„Mr.Hooke stellte eine grafische Methode vor, einen Bogen zu zeichnen, der jedes mögliche Gewicht tragen könne. Gefragt, ob er davon auch eine Vorführung machen könne, antwortete er, dass er dies vor dem Präsidenten getan habe, der bei dieser Zusammenkunft nicht anwesend war.“70
Am 19. Januar 1671 heisst es:
„Dr.Wren führte dem Präsidenten die spezielle Linie vor, die ein Bogen beschreibt, der geeignet ist, jedwedes Gewicht zu tragen. […] Als Mr. Hooke zu seiner Vorführung desselben Problems gerufen wurde erklärte er, dass er dem Präsidenten bereits deren Quintessenz erläutert habe. Dieser habe jedoch den Wunsch geäußert, dass er sie auch schriftlich vorlege, damit sie eingehender und bequemer untersucht werden könne.“71
Erst elf Monate später wird die geheimnisvolle Lösung einen Namen erhalten, obwohl die Details immer noch nicht offenbart werden. Der Eintrag vom 7. Dezember 1671 lautet:
„Mr.Hooke zeichnete die Gestalt des Bogens einer Kuppel zum Tragen unterschiedlicher Lasten und deutete sie als Konoid einer kubischen Parabel. Er ergänzte, dass damit alle architektonischen Probleme von Bögen und Strebepfeilern bestimmt werden könnten.“72
Es handelt sich um die auf der Analogie Bogen – Kettenlinie basierende Lösung, die
„(zehn von den hundert Erfindungen möchte ich veröffentlichen, wenn auch wahrscheinlich nicht in derselben Reihenfolge, sondern so, wie ich dazu Gelegenheit und Muße finde. Ich hoffe, dass die meisten von ihnen der Menschheit nutzen werden, da sie bis jetzt unbekannt und neu sind).“74
betrifft die zweite Invention, die Bogen:
„Die wahre mathematisch und mechanisch definierte Form aller Arten von Bögen zum Bauen, mit dem jeweils erforderlichen, passenden Strebepfeiler. Ein Problem, dem sich bislang kein Autor von Architekturtraktaten jemals gestellt hat.75
Mit der Analogie Bogen – Kettenlinie stand er zu seiner Zeit nicht allein: Mit demselben Thema beschäftigten sich unter anderem David
Die Gründe für dieses Interesse an Gewölben und Kuppeln sind klar: In Verbindung mit dem Wiederaufbau nach dem Great Fire von 1666 und insbesondere mit dem Kuppelentwurf für die St. Paul’s Cathedral formulierten
Neben den schriftlichen Quellen soll hier auch die tatsächlich gebaute Architektur berücksichtigt werden. Die Kuppel der St. Paul’s Cathedral zeugt von einer guten Beherrschung der konstruktiven Techniken, obwohl ihre Konstruktionsweise im Vergleich zu den bekannten Beispielen in
Um in jener Zeit eine weitergehende Beschäftigung mit dem mechanischen Verhalten von Bögen, Gewölben und Kuppeln zu finden, muss man nach
„Das ist eines der schwierigsten Probleme in der Architektur, nämlich die Kraft zu kennen, welche die Pfeiler der Gewölbe haben müssen, um deren Schub auszuhalten. Die Architekten haben bis heute keine gesicherte Regel gefunden, um sie zu bestimmen.“79
Wo die Architekten scheiterten, könnten endlich die Mechaniker Erfolg haben.
Philippe de
Darüber hinaus ist bemerkenswert, dass bereits die einfache Lektüre dieser Texte die Hintergründe verrät, welche
„würden alle Gewölbesteine mit derselben Kraft ganz in Richtung des Zentrums des Gewölbes geschoben“89
dann würde dieses Gewölbe keinen Druck auf die Widerlager ausüben,
„denn der Schlussstein und die ihm benachbarten, darüberliegenden Gewölbesteine würden nicht mehr Kraft ausüben als wenn sie alle miteinander verbunden wären und als wenn sie nur einen festen Körper darstellen würden, von dem man die Kraft bestimmen müsste wie die eines einzigen ganz geraden Steines, der so viel wiegen würde wie alle Gewölbesteine zusammen und waagrecht auf den Pfeilern gelagert wäre.“90
Das verwendete Modell beruht auf der Annahme einer monolithischen Architektur „ein einziger Stein“ (une seule pierre), auch wenn diese aus kleinformatigen Materialien wie Steine oder Ziegel gefügt ist. Das Diskrete, das sich wie das Kontinuum verhält, eine scheinbar widersprüchliche Konstruktionsvorstellung, stellte die Grundlage für die stereotomische Kunst dar. Diese Aspekte wurden allerdings in der Proposition 125 nicht mehr thematisiert, weshalb die im Traité de mécanique verwendete Beweisstrategie unverständlich blieb.
Beachtenswert ist auch das von
„[DeLa Hire] sah etwas, aber das, was er hätte sehen können, verstand er nicht.“92
Tatsächlich markiert der von
4.6 Die science des ingénieurs
An der 1747 in
Der neue „mechanische“ Weg schien – zumindest den Intentionen nach – eingeschlagen worden zu sein. Die Überzeugung, man habe die Phase der „Kunstregeln“ hinter sich gelassen und sei endlich zu einer Kooperation zwischen Kunst und Wissenschaft gelangt, kennzeichnet einen Großteil der damaligen Literatur. Es ist interessant zu beobachten, dass unter den Verfechtern des Neuen, die dieses Neue aber nur vermeintlich durchdrangen, drei „Erklärungsstrategien“ großen und unmittelbaren Erfolg unter den Architekten hatten.
Als erste Erklärungsstrategie beobachtet man zunächst die Ungeduld, endlich eine allumfassende Antwort zu finden. Es ist das Lied der Sirenen des „Kein Ignorabimus“ und der universellen Formeln, die jedes Rätsels Lösung sind. Dieser Drang verwandelte die Kettenlinie in eine bequeme, allgemein anerkannte Antwort, die aber von den wenigsten verstanden und z. B. nur verspätet von der Académie d’Architecture in
„die als Fundament dieser wichtigen Theorie [des Gewölbeschubes] dienen müsste und die anscheinend von fast allen, die über dieses Thema gearbeitet haben, ignoriert worden ist.“94
Die bereits 1717 formulierte und unter anderem von Giovanni
Die zweite Erklärungsstrategie entsprang der Überzeugung, das Verborgene mit Hilfe der Archäologie aufdecken zu können. Ein markantes Beispiel ist der von Giovanni Battista
Die Leidenschaft für die Archäologie und besonders die Versuchung zu enthüllen, führt dazu, etwas zu sehen, was gar nicht existent ist. Diesem Trugschluss unterlagen einige Archäologen des 19. und viele Epigonen des 20. Jahrhunderts. „Iscrutatori dell’intimo delle cose,“ wie Colantonio
Die letzte Erklärungsstrategie ist das alte Adagio der imitatio naturae: Wo die mathematischen Aspekte den meisten unzugänglich und die Integralrechnung den calculatores überlassen blieb, hoben die einen diese, die anderen jene mechanischen Vorstellungen aufs Schild.97 In dieser „Freizone“ konnte man sich auf gemeinsame Elemente verständigen: so wurden Kuppeln mit Apfelsinen oder Eiern verglichen98 und Tonnengewölbe mit der Rinde eines Baumes. Hinter manchen Vergleichen steckte eine kluge experimentelle Anschauung: man denke zum Beispiel an die Analogien Kuppel – Schädel oder Herzmuskel – Ringanker, die der intensiven Zusammenarbeit zwischen
Es handelt sich um vermeintlich simple Analogien, die im Laufe des 19. Jahrhunderts Bestandteil eines Repertoires der Mécanique pour le peuple wurden. Dieses fand vor allem unter den Ingenieuren und Architekten große Verfechter und spielte eine unverzichtbare Rolle in der Vermittlung zwischen Experten und Publikum. Diejenigen, die zwischen dem 18. und 19. Jahrhundert jene „Abbildungen des Verborgenen“ schufen, verstanden von der Gewölbemechanik nicht viel mehr als ein guter Architekt des 17. Jahrhunderts. Aber sie hatten gelernt, den Blick nicht nur auf die Form und die Farbe der Architektur, sondern auch auf ihre Mechanik zu lenken.
Das mechanische Alphabet, das Christopher
Die Leçons données à l’École des Ponts et Chaussées sur l’application de la mécanique à l’établissement des constructions et des machines (1826) von Louis
Danksagung
Ich danke Marcus Popplow für die deutsche Übersetzung des Textes.
Bibliographie
Agrippa, C. (1583). Trattato di Camillo Agrippa Milanese di trasportar la guglia in su la piazza di San Pietro. Rom: Francesco Zanetti.
Alberti, L. B. (1485). De re aedificatoria. Florenz: Nicolò di Lorenzo Alemanno.
- (1912). Zehn Bücher über die Baukunst. Wien; Leipzig: Hugo Heller.
- (1966). L’architettura [De re aedificatoria]. Testo latino e traduzione a cura di Giovanni Orlandi. Introduzione e note di Paolo Portoghesi. Mailand: Il Polifilo.
Aristoteles (1936). Mechanical problems, in Idem, Minor works. With an English translation by W. S. Hett. London/Cambridge, Mass: W. Heinemann/Harvard University Press.
Baldi, B. (1590). Descrittione del Palazzo Ducale di Urbino. In: Versi e prose Venedig: Francesco de’ Franceschi 503-573
- (1612a). De verborum Vitruvianorum significatione, sive perpetuus in M. Vitruvium Pollionem commentarius. Augustae Vindelicorum: ad insigne Pinus.
- (1612b). Scamilli impares Vitruviani, a Bernardino Baldo Urbinate noua ratione explicati (...). Augustae Vindelicorum: ad insigne Pinus.
- (1621). In mechanica Aristotelis problemata exercitationes. Adiecta succinta narratione de autoris vita et scriptis. Moguntiae: Viduae Ioannis Albini.
- (1724). Memorie concernenti la città di Urbino. Roma: Salvioni.
- (1998). Le vite de’ matematici. Edizione annotata e commentata della parte medievale e rinascimentale, a cura di Elio Nenci. Mailand: Franco Angeli.
- (2010). In mechanica Aristotelis problemata exercitationes. Bd. I: Testo latino riveduto e corretto con traduzione italiana a fronte. Bd. II: Edizione anastatica. Mailand: FrancoAngeli.
Barbaro, D. (1556). I dieci libri dell’architettura di M. Vitruvio, tradutti et commentati da Monsignor Barbaro. Venedig: Marcolini.
- (1567a). I dieci libri dell’architettura di M. Vitruvio tradutti e commentati da Monsignor Barbaro, eletto patriarca d’Aquileggia. Venedig: F. de’ Franceschi & G. Chrieger.
- (1567b). M. Vitruuii Pollionis De architectura libri decem, cum commentariis Danielis Barbari. Venedig: apud Franciscum Franciscium Senensem, & Ioan. Crugher Germanum.
Becchi, A., D. Bertoloni Meli, D. B.M. (2013). Guidobaldo del Monte (1545-1607). Theory and Practice of the Mathematical Disciplines from Urbino to Europe. Berlin: Edition Open Access.
Becchi, A., H. Rousteau-Chambon, H. RC. (2013). Philippe de La Hire entre architecture et sciences. Paris: Picard.
Becchi, A. (1999). Between ,natural‘ and structural mechanics. In: Applied Mechanics in the Americas Ed. by D. Pamplona. Philadelphia/Rio de Janeiro: American Academy of Mechanics/Brazilian Society of Mechanical Sciences 507-510
- (2002). Chambre H. Per una storia del costruire. In: Degli archi e delle volte. Arte del costruire tra meccanica e stereotomia Ed. by A. Becchi, F. Foce. Venedig: Marsilio 19-127
- (2004). Q. XVI. Leonardo, Galileo e il caso Baldi: Magonza, 26 Marzo 1621. Venedig: Marsilio.
- (2005). Vaults in the Air: Signor Fabritio’s English Theory. In: Essays in the history of the theory of structures Ed. by S. Huerta. Madrid: Instituto Juan de Herrera 45-49
- (2006). Eggs, turnips and chains: rhetoric and rhetoricians of architecture. In: Practice and Science in Early Modern Italian Building. Towards an Epistemic History of Architecture Ed. by H. Schlimme. Mailand: Electa 97-112
- (2008a). „Taccia dunque la turba de gli Architetti pratici ...“. Henry Wotton und der Abt von Guastalla. In: Wissensformen Ed. by W. Oechslin. Zürich: gta-Verlag 100-107
- (2008b). Imaginer l’entasis. Constructions, définitions, malentendus dans les traités de la Renaissance. In: La colonne. Nouvelle histoire de la construction Ed. by R. Gargiani. Lausanne: École Polytechnique Fédérale de Lausanne 149-163
- (2008c). Les paradoxes (historiographiques) de la vis columnarum. In: La colonne. Nouvelle histoire de la construction Ed. by R. Gargiani. Lausanne: École Polytechnique Fédérale de Lausanne 203-219
- (2009). Juxta textum Vitruvii et mentem Newtonii. Das neue Wissen und das „Räthsel der Architektur“. In: Architekt und/versus Baumeister Ed. by W. Oechslin. Zürich: gta Verlag 40-49
- (2010). La doppia vita di una ‚mauvaise règle‘. La regola di Derand tra Leon Battista Alberti e Simone Stratico. In: Geometry and Proportion in Structural Design. Essays in Ricardo Aroca’s Honour Ed. by P. Cassinello, S. Huerta, S. H., de Prada Poole S.. Madrid: Ed. Lampreave 123-139
- (2011). Cantieri d’inchiostro. Meccanica teorica e meccanica chirurgica nella seconda metà del Cinquecento. In: Studi su Domenico Fontana Ed. by G. Curcio, N. Navone, N. N.. Mendrisio: Mendrisio Academy Press, Silvana Editoriale 91-103
- (2013a). „…zoticamente non intendendo le Mechaniche“. La scientia aedificandi ai tempi di Guidobaldo del Monte. In: Guidobaldo del Monte (1545-1607). Theory and Practice of the Mathematical Disciplines from Urbino to Europe Ed. by A. Becchi, D. Bertoloni Meli, D. B.M.. Berlin: Edition Open Access 241-263
- (2013b). Idées manuscrites, théories imprimées: la mécanique architecturale de Philippe de La Hire. In: Philippe de La Hire entre architecture et sciences Ed. by A. Becchi, H. Rousteau-Chambon, H. RC.. Paris: Picard 177-190
- (2013c). Archimedes’ Bath. In: Archimedes. The Art and Science of Invention Ed. by G. Di Pasquale, C. Parisi Presicce. Florenz: Giunti 115-119
Bedon, A. (1983). Il „Vitruvio“ di Giovan Antonio Rusconi. Ricerche di Storia dell’Arte
- (1996). Giovan Antonio Rusconi: Illustratore di Vitruvio, artista, ingegnere, architetto. Vicenza: Centro Internazionale di Architettura Andrea Palladio.
Benvenuto, E. (1991). An Introduction to the History of Structural Mechanics. New York, Berlin: Springer.
Bernini, D. (2002). Bernardino Baldi e il Palazzo Ducale di Urbino. Accademia Raffaello. Atti e Studi
Birch, T. (1756). The History of the Royal Society of London for Improving of Natural Knowledge …. London: A. Millar.
Bolton, A., H. H. Duncan (1942). The City churches [...] and the five tracts on architecture by Sir Chr. Wren. Drawings, engravings, photographs..
Calegari, G. (2004). Palazzo Mamiani Della Rovere: indagini e scoperte. In: Palazzo Gradari già Palazzo Mamiani Della Rovere. Indagini e scoperte dopo il restauro Ed. by D. Trebbi, S. Bruscia, S. B., Nori S.. Ancona: Futura Officine Grafiche 113-140
Campori, G. (1855). Gli artisti italiani e stranieri negli Stati Estensi. Modena: Tip. Della R.D. Camera.
Coulomb, C. A. (1773). Essai sur une application des règles de maximis et minimis à quelques problèmes de statique, relatifs à l’architecture. Mémoires de mathématique & de physique, présentés à l’Académie Royale des Sciences par divers savans 7: 343-382
Cremona, L. (1872). Le figure reciproche nella statica grafica. Mailand: Hoepli.
Crescimbeni, G. M. (2001). La vita di Bernardino Baldi, Abate di Guastalla. Urbino: a cura di Ilaria Filograsso, QuattroVenti.
Culmann, K. (1866). Die graphische Statik. Zürich: Meyer & Zeller.
Daniello, B. (1568). Dante con l’espositione di M. Bernardino Daniello da Lucca, sopra la sua Comedia dell’Inferno, del Purgatorio, & del Paradiso; nuouamente stampato & posto in luce…. Venedig: Pietro da Fino.
Danyzy, A. A. H. (1778). Méthode générale pour déterminer la résistance qu’il faut opposer à la poussée des voûtes. In: Histoire de la Société Royale des Sciences établie à Montpellier Languedoc: Jean Martel Ainé
Dee, J. (1570). Brief an den Leser. In: Libro del modo di dividere le superficie attribuito a Machometo Bagdedino. Mandato in luce la prima volta da M. Giovanni Dee da Londra, e da M. Federico Commandino da Urbino […] Pesaro: Girolamo Concordia
de Guevara, G. (1627). Ioannis de Guevara Cler. Reg. Min in Aristotelis Mechanicas Commentarij: una cum additionibus quibusdam Ad eandem materiam pertinentibus. Roma: Iacobum Mascardum,.
del Monte, G. (1581). Le mechaniche (…) tradotte in volgare dal Sig. Filippo Pigafetta. Venetia: appresso Francesco di Franceschi Sanese.
Derand, F. (1643). L’Architecture des voûtes, ou l’art des traits et coupe des voûtes …, par François Derand. Paris: S. Cramoisy.
Diderot, D., J. d’Alembert (1778). Encyclopédie ou dictionnaire raisonné des sciences, des arts et des métiers. A. Genève: chez Pellet.
Duhem, P. (1906). Les origines de la statique. Paris: Hermann.
- (1906–1913). Études sur Léonard de Vinci: ceux qu’il a lus et ceux qui l’ont lu. Paris: Hermann.
Engel, H. (2006). Dantes Inferno. Zur Geschichte der Höllenvermessung und des Höllentrichtermotivs. München-Berlin: Deutscher Kunstverlag.
Euklid (1570). The Elements of Geometrie. London: Daye, I..
- (1572). Euclidis Elementorum Libri XV. Unà cum Scholijs antiquis. À Federico Commandino Urbinate nuper in Latinum conversi commentarijsque quibusdam illustrati. Pisauri: Iacobus.
Evelyn, J. (1664). An Account of Architects and Architecture, together with An Historical, and Etymological Explanation of certain Tearms particularly affected by Architects, in Roland Fréart Sieur de Chambray, A Parallel of the Antient Architecture with the Modern […]. London: Tho Roycroft.
Fontana, C. (1694). Templum Vaticanum et ipsius origo. Rom: Buagni.
Fontana, D. (1590). Della Trasportatione dell’Obelisco Vaticano (…). Roma: Domenico Basa.
- (1979). Della Trasportatione dell’Obelisco Vaticano, a cura di Adriano Carugo, con un’introduzione di Paolo Portoghesi. Mailand: Il Polifilo.
Forest de Bélidor, B. (1729). La science des ingénieurs dans la conduite des travaux de fortification et d’architecture civile. Paris: C.-A. Jombert.
Frézier, A.-F. (1737–1739). La théorie et la pratique de la coupe des pierres et des bois pour la construction des voûtes, et autres parties des bâtiments civils et militaires, ou traité de stéréotomie à l’usage de l’architecture (...) par Frézier..
Gabrieli, G. (1996). Il carteggio Linceo. Roma: Accademia nazionale dei Lincei.
Galilei (1638). Discorsi e dimostrazioni matematiche intorno a due nuove scienze attenenti alla mecanica et i movimenti locali. Leiden: Elsevirii.
- (1968). Le opere. Florenz: Barbera.
Gerhardt, C. I. (1855). Leibnizens mathematische Schriften. Halle: H.W. Schmidt.
Giambullari, P. (1544). De’l Sito, Forma, e Misure, dello Inferno di Dante. Florenz: Neri Dortelata.
- (1551). Lezzioni di M. Pierfrancesco Giambullari, lette nella Accademia fiorentina. Florenz: Lorenzo Torrentino.
Girard, P.-S. (1798). Traité analytique de la résistance des solides et des solides d’égale résistance, auquel on a joint une suite de nouvelles expériences sur la force et l’élasticité spécifiques des bois de chêne et de sapin. Paris: Didot.
Gregory, D. (1697). Catenaria. Ad Reverendum Virum D. Henricum Aldrich S.T.P. Decanum Aedis Christi Oxoniae. Philosophical Transactions 19: 637-652
Hevelius, J. (1673). Machinae coelestis pars prior: organographiam, sive instrumentorum astronomicorum omnium, quibus auctor hactenus sidera rimatus, ac dimensus est, accuratam delineationem et descriptionem (…) exhibens. Gedani: Simon Reiniger.
Heyman, J. (1998). Hooke’s Cubico-Parabolical Conoid. Notes and Records of the Royal Society of London 1(52): 39-50
Hooke, R. (1676). A Description of Helioscopes and Some Other Instruments. London: Martyn.
La Hire, P. (1690). Traité de la coupe des pierres..
- (1692). Remarques sur l’époisseur qu’on doit donner aux pieds droits des voutes et aux murs des dômes ou voutes de four. Manuskript, Procès-verbaux de l’Académie Royale d’Architecture, 27. Oktober 1692; Transkription in (Lemonnier 1911–1929, Bd. 2, S. 345–349).. Paris: Archiv des Institut de France.
- (1695). Traité de mécanique, où l’on explique tout ce qui est nécessaire dans la pratique des Arts, et les proprietés des corps pesants lesquelles ont eu plus grand usage dans la Physique. Paris: Imprimerie Royale.
- (1698). Architecture civile. Manuskript 725. London: RIBA Library.
- (1711). Règle générale pour déterminer la largeur de la face des piédroits des arcs, lesquels puissent résister à l’effort avec lequel l’arc les escarte, ce qu’on appelle l’effort de la poussée sur la hauteur donnée de ses piédroits. Manuskript, Procès-verbaux de l’Académie Royale d’Architecture. Paris: Archiv des Institut de France.
- (1712). Sur la construction des voûtes dans les édifices. Mémoires de l’Académie Royale des Sciences
Lemonnier, H. (1911–1929). Procès-verbaux de l’Académie Royale d’Architecture (1671–1793)..
Lévy-Leblond, J.-M. (2006). Galilée dans l’Enfer de Dante. In: La vitesse de l’ombre. Aux limites de la science Paris: Éditions du Seuil 80-85
Lohr, C. H. (1974). Renaissance Latin Aristotle Commentaries: Authors A-B. Studies in the Renaissance 21: 228-289
- (1975–1982). Renaissance Latin Aristotle Commentaries: Authors C. Authors D-F. Authors G-K. Authors L-M. Authors N-Ph. Authors Pi-Sm. Authors So-Z. Renaissance Quarterly
Malke, L.S. (2000). Dantes Göttliche Komödie. Drucke und Illustrationen aus sechs Jahrhunderten. Berlin: Kunstbibliothek-Staatliche Museen Berlin.
Mercati, M. (1589). De gli obelischi di Roma. Roma: Domenico Basa.
Mögling, D. (1629). Mechanischer Kunst-Kammer Erster Theil (…). Frankfurt am Main: Merian.
Monte, Guidobaldo del (1577). Mechanicorum liber. Pisauri: H. Concordiam.
- (1588). In duos Archimedis aequeponderantium libros paraphrasis scholijs illustrata. Pisauri: H. Concordiam.
- (1592). Meditatiunculae Guidi Ubaldi […]. Paris, MS Lat. 10246: Bibliothèque Nationale de France.
Narducci, Enrico (1886). Vite inedite di Matematici Italiani scritte da Bernardino Baldi. Bullettino di Bibliografia e di Storia delle Scienze Matematiche e Fisiche XIX: 464-473
Navier, L. (1826). Résumé des leçons données à l’École des Ponts et Chaussées sur l’application de la mécanique à l’établissement des constructions et des machines. Paris: F. Didot père et fils.
Neumeyer, Fritz (2002). Quellentexte zur Architekturtheorie. München/London/New York: Prestel.
Nix, L., W. Schmidt (1900). Heron von Alexandria, Mechanik und Katoptrik,. In: Heronis Alexandrini opera qvae svpersvnt omnia Ed. by G. Schmidt. Leipzig: Teubner
Oechslin, W. (2002). Philosophemur: Zu Henry Wottons Elements of Architecture (1624). In: Lezioni di metodo. Studi in onore di Lionello Puppi Ed. by L. Olivato. Vicenza: Terra Ferma 251-270
Palladio, A. (1570). I quattro libri dell’architettura. Venetia: Dominico de’ Franceschi.
Pappus (1588). Pappi Alexandrini mathematicae collectiones (…). Pisauri: H. Concordiam.
Peterson, M.A. (2002). Galileo’s Discovery of Scaling Laws. American Journal of Physics
Piasentin, M. (1978–1979) Giovan Antonio Rusconi. mathesis. IUAV
Pigafetta, F. (1586). Discorso di M. Filippo Pigafetta d’intorno all’historia della Aguglia & alla ragione del muoverla. Roma: Bartolomeo Grassi.
Piranesi, Francesco (1780). Raccolta de’ Tempj Antichi. Opera di Francesco Piranesi Architetto Romano..
Plinius Secundus, Caius (1832). Historia naturalis ex recensione I. Harduini et recentiorum adnotationibus. Augustae Taurinorum: Pomba.
Poinsont, L. (1877). Éléments de Statique. Paris.
Poleni, G. (1748). Memorie istoriche della gran cupola del Tempio Vaticano (…). Padua: Stamperia del Seminario.
Prinz, W. (1983). Informazione di Filippo Pigafetta al Serenissimo di Toscana per una stanza da piantare lo studio di architettura militare. In: Gli Uffizi. Quattro secoli di una galleria Ed. by P. Barocchi, G. Ragionieri. Florenz: Olschki 343-353
Renn, J., P. Damerow (2010). Guidobaldo del Monte’s Mechanicorum liber. Berlin: Edition Open Access.
- (2012). The Equilibrium Controversy: Guidobaldo del Monte’s Critical Notes on the Mechanics of Jordanus and Benedetti and their Historical and Conceptual Background. Berlin: Edition Open Access.
Robinson, H. W., W. Adams (1935). The Diary of Robert Hooke, 1672–1680 (…). London: TaylorFrancis.
Ronchini, A. (1873). Lettere di Bernardino Baldi cavate dagli autografi che sono a Parma nell’Archivio di Stato. Parma: R. Deputazione di Storia Patria.
Rondelet, J.-B. (1802–1817). Traité théorique et pratique de l’art de bâtir. Paris: J.-B. Rondelet.
Rose, P.L., S. Drake (1971). The Pseudo-Aristotelian Questions of Mechanics in Renaissance Culture. Studies in the Renaissance 18: 65-104
Rusconi, G. A. (1590). Della architettura di Gio. Antonio Rusconi. Venedig: Gioliti.
Scamozzi, V. (1615). Dell’idea della architettura universale. Venetiis: Scamozzi.
Schöller, W. (1993). Die Académie royale d’architecture, 1671–1793. Anatomie einer Institution. Köln: Böhlau-Verlag.
Serrai, A. (2002). Bernardino Baldi. La vita, le opere. La biblioteca. Mailand: Bonnard.
Settle, T. B. (2001). Experimental sense in Galileo’ early works and its likely sources. In: Largo campo di filosofare. Eurosymposium Galileo 2001 Ed. by J. Montesinos, C. Solís. La Orotava: Fundación Canaria Orotava de Historia de la Ciencia 831-849
- (2002). Dante, the Inferno and Galileo. In: Pictorial means in early modern engineering, 1400–1650 Ed. by W. Lefèvre. Berlin: Max-Planck-Institut für Wissenschaftsgeschichte, Preprint 93 139-157
Shute, J. (1563). The First and Chief Groundes of Architecture. London: T. Marshe.
Silberschlag, J. E. (1786). Ausführlichere Abhandlung der Hydrotechnik des Wasserbaues, Teil II. Wien: Johann Thomas Edlen von Trattern.
Smith, L. P. (1907). The Life and Letters of Sir Henry Wotton. Oxford: Clarendon Press.
Soo, L. M. (1998). Wren’s ‚Tracts‘ on Architecture and other Writings. Cambridge: Cambridge University Press.
Stirling, J. (1717). Methodus disponendi quotcunque Sphaeras in Fornicem. Et inde Demonstratur Proprietas praecipua Curvae Catenariae. In: Lineae Tertii Ordinis Neutonianae, sive Illustratio Tractatus D. Neutoni De Enumeratione Linearum Tertii Ordinis. […] Ed. by J. Stirling. Oxoniae: E Theatro Sheldoniano, Impensis Eduardi Whistler Bibliopolae Oxoniensis 11-14
Strano, G. (2008). Il telescopio di Galileo. Lo strumento che ha cambiato il mondo. Florenz: Giunti.
Tartaglia, Niccolò (1546). Quesiti e inventioni diverse. Venetia.
Tassora, R. (2001) Le Meditatiunculae de rebus mathematicis di Guidobaldo del Monte. phdthesis. Università di Bari
Truesdell, Clifford Ambrose (1960). The Rational Mechanics of flexible or elastic bodies 1638–1788. Introduction to L. Eulerii Opera Omnia. Basel: Birkhäuser.
Vitruv (1488). De architectura libri decem. Roma.
Waller, R. (1705). The Life of Dr. Robert Hooke. In: The Posthumous Works of Robert Hooke… Ed. by R. Waller. London: S. SmithB. Walford I-XXVIII
Wotton, H. (1624). Elements of Architecture. Collected by Henry Wotton Knight, from the Best Authors and Examples. London: I. Bill.
- (1968). The Elements of Architecture. A Facsimile Reprint in the First Edition (London, 1624). Charlottesville: University Press of Virginia.
Wren, S. (1750). Parentalia or, Memoirs of the Family of the Wrens. London: T. OsbornR. Dodsley.
Yates, Frances (1969). Theatre of the World. London: Routledge & Kegan Paul.
Zorzi, G. (1956–1957). Altre due perizie inedite per il restauro del Palazzo Ducale di Venezia dopo l’incendio del 20 Dicembre 1577. Atti dell’Istituto Veneto di Scienze, Lettere ed Arti 115: 169-170
Fußnoten
Dieser Beitrag ist z. T. folgenden Aufsätzen des Autors entnommen: Becchi 2008a, Becchi 2009, Becchi 2013a.
Eines der längsten Teleskope, das in Danzig nach einem Entwurf von Hevelius errichtet wurde, maß 45 Meter. Eine Abbildung findet sich in dem Werk Johannes Hevelius (1673, Abb. AA und BB). Vgl zu diesem und anderen Aspekten der Geschichte des Fernrohres Strano 2008. In diesem Band wird, in dem von Jim und Rhoda Morris verantworteten Abschnitt mit dem Titel Riprodurre il telescopio di Galileo (S. 58–61), der Aufbau des (auf etwa 1610 datierten) Teleskopes beschrieben, das Galilei Cosimo II zum Geschenk gemacht hatte.
„Quanto poi il slamar il detto muro, dico similmente essere impossibile, prendendo essempio dalla stadera […] con questo esempio se somigliaremo il Palazzo alla stadera, troveremo in lui le medesime parti, che habbiamo nominato in lei, et saranno tali. Diremo prima che l’oncino sarà in quello luogo del terrazzo del gran Consiglio […].“, Zorzi 1956–1957, 168. Zorzi erläutert das hier verwendete Wort ‚slamar‘ in einer Anmerkung: „Im venezianischen Dialekt bedeutet ‚slamar‘ ‚gleiten, rutschen‘.“, vgl. Zorzi 1956–1957, 168, Anm. 8.
Zu Rusconi vgl. Piasentin 1978–1979 und Bedon 1983; auch Bedon 1996, IX–XXII.
Vgl. Tartaglia 1546, Buch IX, Frage XXXVIII, 126v. Diese Aufgabe entspricht einem Brief an Girolamo Cardano vom 4. August 1539. Rusconi wird auch in anderen Passagen von Tartaglias Werk zitiert.
Vgl. Scamozzi 1615, Teil II, Buch VIII, 320: „Diese Kraft und Ebenmäßigkeit des kuppelförmigen Gewölbes können wir auch durch Erfahrungen mit natürlichen Objekten kennenlernen, insbesondere mit dem Ei; dieses hat aufgrund seiner Natur eine sehr dünne und verletzliche Schale, dennoch ist es der Kraft des Menschen nicht möglich, sie zu zerbrechen, wie schon Plinius bemerkte […] wir haben ausprobiert, dass drei auf einen Tisch gestellte Eier, oben und unten mit etwas Wachs versehen, das Gewicht eines metallenen Mörsers von mehr als 150 libre halten“.
Vgl. Due lezioni all’Accademia Fiorentina circa la figura, sito e grandezza dell’Inferno di Dante in: Galilei 1968, Bd. IX, 31–46 und 47–57. Die beiden Vorlesungen sind leicht online zugänglich, beispielsweise über die Seite http://www.liberliber.it. Vgl. für kritische Untersuchungen Settle 2001; 2002; Lévy-Leblond 2006 und Peterson 2002. Petersons Text ist online verfügbar über: http://www.mtholyoke.edu/courses/mpeterso/galileo/scaling8.pdf.
„Ma lasciamo stare l’architettura, e veggiamo se tal fabbrica può reggersi, che, al parer mio, troveremo non potere; perché, ponendo esso che il burrato si alzi su con le sponde equidistanti tra di loro, si troveranno le parti superiori prive di sostegno che le regga, il che essendo, indubitatamente rovineranno: perciò che, essendo che le cose gravi, cadendo, vanno per una linea che dirittamente al centro le conduce, se in essa linea non trovano chi le impedisca e sostenga, rovinano e caggiono (…). Se dunque sopra questa buca puntano e si sostengono le altre rocce, è necessario che le mura che le deono sostenere non siano fuori del perpendicolo che tende al centro. Questo inconveniente non è nell’architettura del Manetti.“, Galilei 1968, Bd. IX, 52–53.
„Qui ci potrebbe essere opposto che né l’Inferno si deve credere esser così grande come il Manetti lo pone; essendo che, sì come alcuni hanno sospettato, non par possibile che la volta che l’Inferno ricuopre, rimanendo sì sottile quant’è di necessità se l’Inferno tanto si alza, si possa reggere, e non precipiti e profondi in esso Inferno; e massime, oltre al rimanere non più grossa dell’ottava parte del semidiametro, che sono miglia 405 incirca, essendovi ancora da levarne per lo spazio della grotta degli sciagurati, ed essendoci molte gran profondità di mari. Al che facilmente si risponde, che tal grossezza è suffizientissima: perciò che, presa una volta piccola, fabricata con quella ragione, se arà di arco 30 braccia, gli rimarranno per la grossezza braccia 4 in circa, la quale non solo è bastante, ma quando a 30 braccia di arco se gli desse un sol braccio, e forse
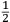 , non che 4, basteria a sostenersi; onde, sapendo noi che pochissime miglia, anzi che meno di un sol miglio, si profondano i mari, se creder doviamo a i più periti marinari, e potendo assegnare quante miglia ci pare per la grotta de gli sciagurati, non essendogli data dal Poeta determinata misura, quando ancora ponessimo tra questa e la profondità de i mari importare 100 miglia, nulla di meno rimarrà detta volta grossissima, e più assai che non è necessario per sostenersi.“, Galilei 1968, Bd. IX, 54–55.
, non che 4, basteria a sostenersi; onde, sapendo noi che pochissime miglia, anzi che meno di un sol miglio, si profondano i mari, se creder doviamo a i più periti marinari, e potendo assegnare quante miglia ci pare per la grotta de gli sciagurati, non essendogli data dal Poeta determinata misura, quando ancora ponessimo tra questa e la profondità de i mari importare 100 miglia, nulla di meno rimarrà detta volta grossissima, e più assai che non è necessario per sostenersi.“, Galilei 1968, Bd. IX, 54–55.
Peterson (2002, 2) schreibt nachdrücklich: „Ich werde zeigen, dass der Schlüssel zu Vielem, was in den ‚Zwei neuen Wissenschaften‘ sonderbar klingt, in zwei weitgehend unbeachteten frühen Vorlesungen liegt, die Galileo zu Gestalt, Ort und Größe von Dantes Inferno gegeben hat.“ („I will show that the key to much of what is strange in Two New Sciences is to be found in two rather neglected early lectures given by Galileo on the shape, location, and size of Dante’s Inferno“.) Text online verfügbar: http://www.mtholyoke.edu.
Daniello 1568, vgl. Giambullari 1544; 1551. Vgl. zu diesen Themen und der entsprechenden Ikonographie Engel 2006 und Malke 2000.
„le macchine che riescono in piccolo, riusciranno anche in grande“.
„[…] conviene che io confessi di non aver saputo spiegare il mio concetto con quella evidenza che è necessaria per ben dichiararsi, e massime quando si arrecano proposizioni remote dalle opinioni comuni. Dico per tanto che l’intenzione mia fu molto diversa, anzi del tutto contraria al senso che V.S. ne ha cavato.“, G. Galilei, Brief an Antoine de Ville, Arcetri, März 1635, vgl. Galilei 1968, Bd. XVI, 196. Fulgenzio Micanzio beschreibt die Persönlichkeit von Antoine de Ville in einem Brief an Galileo vom 24. Februar 1635, Galilei 1968, Bd. XVI, 177–178: „Dies ist ein französischer Edelmann, Ingenieur und, soweit ich beurteilen kann, sehr gebildet nicht nur in den mechanischen, sondern in allen mathematischen Wissenschaften und kenntnisreich bezüglich der guten Autoren, aber, wie diejenigen, die es wissen, unerfahren.“
Pigafetta, Brief an Giulio Savorgnan in del Monte 1581, Blatt a2v.
„un magazino di machine bellicose, et da mover pesi, havendone ella fabricate di sua industria forse dodici di maniere differenti, parte da strascinare, et parte da alzare con pochissima forza smisurati pesi.“, Pigafetta in: del Monte 1581, Blatt bv–b2r.
„un ridotto di persone virtuose, et un albergo di soldati, et di dottori“. Pigafetta in del Monte 1581, Blatt bv.
Vgl. Prinz 1983. Auf S. 351–353 ist die Transkription der Informazione Pigafettas abgedruckt, die folgendermaßen endet: „Und wenn er zu verstehen geben wird, über diese Erfindungen zu verfügen, sowohl Instrumente, als auch militärische Modelle, wird man in kurzer Zeit den gesamten Saal voller auserwählter Dinge vorfinden, und er wird sogar Zugbrücken, Bootsbrücken, ponti d’odri und unterschiedliche aus Fässern gefertigte Brücken enthalten, sowie freschi und Brustwehren, die jedem Kanonenschlag widerstehen, und sichere, rollbare Schutzschilder und Artillerie, die aus vorgefertigten Elementen zusammengesetzt ist, und sogar ohne Verwendung von Metall wirksam ist, und ähnliches […].“
Archivio di Stato di Venezia, Secreta, Materie miste notabili, reg. 13, Blätter 55v–56: „Aufgaben 29 Aufgaben, die Giulio Savorgnan 1542 durch seinen zwergwüchsigen Knaben dem berühmten Nicolò Tartaglia stellen ließ, um ihn über unterhaltsame Dinge nachdenken zu lassen“; vgl. auch den Ausstellungskatalog Ambiente scientifico veneziano tra cinque e seicento, Testimonianze d’archivio (27. Juli–6. Oktober 1985), Venezia, Tip. Helvetia 1985, 35 und die Abhandlung von Adriano Carugo „Gli obelischi e le macchine nel Rinascimento“, in: Fontana 1979, LVII–LVIII, insbesondere Anm. 87.
„E se si rompesse?“, vgl. Mercati 1589, 291.
Aristoteles 1936, eine lange Aristoteles zugeschriebene Schrift.
Baldi war wegen seines besonderen Sprachtalents bekannt und soll mindestens zwölf Sprachen beherrscht haben. Diese außerordentlichen Fertigkeiten erwarb er in seiner Jugend, als er unter der Leitung von Giovanni Antonio Turoneo in Urbino studierte. Darüber hinaus hat das Zusammentreffen mit Giovanni Battista Raimondi, Initiator der Tipografia Medicea Orientale (Rom), eine wichtige Rolle gespielt: Von ihm lernte er Arabisch, was eine Vertiefung seiner akribischen Arbeit an den wissenschaftlichen und literarischen Quellen ermöglichte.
Zu den Aktivitäten Guidobaldos auf dem Gebiet der Architektur vgl. Calegari 2004.
Zu diesem Manuskript vgl. Tassora 2001, frei verfügbar über die Homepage von ECHO http://echo.mpiwg-berlin.mpg.de/content/mpiwglib/pesaro/tassora.
Für ein Verzeichnis der zahlreichen Druckwerke und Manuskripte Baldis vgl. Serrai 2002.
„Monsig.r Abate di Guastalla mi ha fatto sapere che dovendosi rifare ora il Ponte del Baccanello ha una bellissima invenzione di Ponte che volentieri metteria in opra, e desidera esser sentito da V.S. alla quale parlato ch’avrà, o in scritto fattole sapere quello che passa, farai poi anco vedere il modello.“, Brief von Don Ferrante Gonzaga an den Marchese Cornelio Bentivoglio, datiert 1. Mai 1602; vgl. Campori 1855, 29. Don Ferrante erwähnt einen Brief Baldis vom 22 April 1602: „Ich habe an S.r Donesmondi geschrieben, dass er Ihrer Exzellenz etwas von der am Baccanello zu bauenden Brücke erzählt; wenn Sie Gelegenheit haben, an den S.r Marchese zu schreiben, könnten Sie ihm darüber einige Worte mitteilen.“, vgl. Ronchini 1873, 133–134.
Baldi 1612a, ein umfassendes Wörterbuch für die Lektüre Vitruvs; vgl. auch Baldi 1612b.
B. Baldi, Descrizione del Palazzo Ducale d’Urbino, in: Baldi 1724; vgl. auch Baldi 1590. Zu diesem Text vgl. Bernini 2002.
Scarloncino, „scio dixisse aliquando Adrianum Romanum e Polonia reuersum, vbi Vitruuium Palatino cuidam explicauerat, si commentarium Baldi in Polonia adhibere potuissem, aurum quod mecum attuli emunxissem, quia satis fecissem muneri labore nullo.“, De vita et scriptis Bernardini Baldi, cit., Seiten nicht paginiert.
„[…] ed ancorché si trovasse allora lontano di quella città, nondimeno coll’aiuto e della pianta, che egli stesso aveva dapprima cavata, e della sua maravigliosa memoria, la fece con tale esattezza, quale fatta l’avrebbe se si fusse ritrovato in Urbino: fatica riputata utilissima nella professione dell’architettura, imperciocché per essere assai difficile il sito, ove quel palagio è fabbricato, molto riesce malagevole il poter riconoscersi dalla semplice pianta la sua intera bellezza.“, Crescimbeni 2001, 73.
Vgl. Baldi 1621, 110.
Deutsche Übersetzung von Mögling 1629; vgl. Baldi 1621, 91: „Cur eiusdem magnitudinis lignum facilius genu frangatur si quispiam aeque diductis manibus extrema comprehendens fregerit, quam si iuxta genu. Et si terrae applicans pede superposito manu hinc inde diducta confregerit quam prope.“
Deutsche Übersetzung von Mögling 1629; vgl. Baldi 1621, 95: „Quare, quo longiora sunt ligna, tanto imbecilliora fiant, si tolluntur, inflectuntur magis: tametsi quod breue est ceu bicubitum fuerit, tenue, quod vero cubitorum centum crassum?“
„Si dans la théorie de la statique il est permis de regarder les leviers au moyen desquels les mobiles agissent les uns sur les autres comme doués d’une inflexibilité parfaite, cette supposition cesse d’être admissible dans l’application de cette science au calcul des machines, puisque la nature n’a créé aucune substance dont les parties intégrantes ne puissent être séparées les unes des autres par l’action d’un certain effort. Il y a donc deux espèce d’équilibre à considérer dans le levier, et dans les machines qui s’y rapportent; l’un existe entre les efforts opposés qui se contrebalancent, l’autre entre une certaine fonction de ces efforts et la cohérence des parties dont les machines sont composées. On peut assigner rigoureusement les conditions du premier, mais celles du second ne sont assignables que par approximation.“, Girard 1798, IX.
„Pour traiter mathématiquement des corps solides, il fallait tout d’abord, suivant lui, qu’on voulût bien en accepter une définition mathématique. ‚Ma canne, disait-il souvent, n’est pas un corps solide; non-seulement elle peut rompre, mais elle plie, ce qui est cent fois pis‘.“, vgl. J. Bertrand „Notice sur Louis Poinsot“ in: Poinsont 1877, IX–XXVIII.
Kein Kommentator hatte diesem Thema je mehr als zwei Seiten gewidmet, die ausführlichere Behandlung belegt das spezifische Interesse an diesem Thema. Vgl. zur langen Folge von Kommentaren und Übersetzungen der Mechanischen Problemen in der Renaissance Rose and Drake 1971; Lohr 1974; Lohr 1975–1982.
„Modo vt ex hac contemplatione, quæ alias inutilis videtur, aliquam vtilitatem capiamus, ex his quæ contemplabimur, Architecti prudentiores fiant, ist hæc ipsa, de quibus agimus, ad rem ædificatoriam commode aptabimus.“, vgl. Baldi 1621, 98.
Vgl. für die deutsche Übersetzung Alberti 1912, 155. Vgl. Alberti 1485, Buch III. Zu der hier wiedergegebenen Transkription vgl. Alberti 1966, Bd. I; 234–135: „Et enim ducendi arcus rationem traxisse homines hinc puto: nam, cum viderent trabes duas iunctis capitibus posse imis pedibus divaricatis ita firmari, ut mutuo innexu paribusque contra se ponderibus sisterent, placuit inventum, et coeperunt istoc opere displuvia ædificiis tecta apponere. Post id, fortasse cum ex instituto maiorem cooperire aream trabium brevitate nequivissent, intermedium ad sublimia truncorum capita aliquid interposuere, ut essent prope atque apud Græcos littera Π, appositumque ipsum id fortassis cuneum appellavere. Succedente inde argumento multiplicatis cuneis istiusmodi arcus effigiem effectam spectantes probavere, eamque ducendi arcus rationem ad opera lapidea transferentes integrum additamentis arcum effecere.“
Vgl. Becchi 2004.
Henry Wotton (1568–1639), Provost von Eton und lange Zeit Botschafter von Jacob I., König von England und Schottland, in Venedig.
Im Buch von Neumeyer Quellentexte zur Architekturtheorie – Neumeyer 2002 – findet Wotton keinen Platz. Aus der spärlichen Literatur zum Thema sollen folgende Beiträge genannt werden: das ausgezeichnete Essay von Werner Oechslin (2002) Philosophemur: Zu Henry Wottons Elements of Architecture, die Introduction von Frederick Hard in Wotton 1968, sowie das unverzichtbare Werk von Logan Pearsall Smith (1907).
„Brickes moulded in their ordinary Rectangular forme, if they shall be lays one by another in a levell row, betweene any Supporters sustayning the two ends, then all the pieces between, will necessarily sinke, even by their owne naturall Gravity, and much more if they suffer any depression by other waight above them, because their sides being paralell, they have roome to descend perpendicularly, without impeachment, according to the former Theoreme; Therefore to make them stand, wee must either change their Posture, or their Figure, or both.“, siehe Wotton 1624, 47; vgl. auch Baldi 1621, 105–106.
„[...] 29. Gli Automati di Heron, Alessandrino, in 4°. 30. Gli Spiritali del Medesimo, con figure, in 4°. 31. La Prospettiva d’Euclide comentata di Ignatio Danti, in 4°. 32. La Geographia di Maurolico, in 4°. [...] 36. A discourse, in 4°, written by Galileo sopra le cose che nuotono.“, vgl. Smith 1907, Bd. I, 484–486. Leicht identifizierbare Werke, ,Geographia‘ steht für ,Cosmographia‘.
John Dee, Mathematicall Praeface, in: Euklid (1570). Das Werk von Euklid war nicht nur im Laufe der gesamten Renaissance ein unverzichtbares Vorbild, sondern erfuhr auch gerade zu Wottons Zeiten einen grossen verlegerischen Erfolg (im Jahr 1607 entstand sogar die berühmte partielle Übersetzung ins Chinesische von Matteo Ricci und Su Guan Xi).
Vgl. Euklid 1572.
„Sir Henry Wotton in his Concise and Useful Theorems […] the Flower and Crown as it were of all the Sciences Mathematical.“, Evelyn 1664, 118.
„John Dee, Robert Fludd, Inigo Jones. These three personages have never before been placed in a sequence. The next chapter will suggest that the discovery of Vitruvian influences in Dee and Fludd makes necessary a new historical approach to Inigo Jones.“, Yates 1969, 78.
Wie allgemein bekannt hat Yates Wotton in anderen Schriften behandelt, ohne aber diese Forschungslinie zu vertiefen.
„preferring like a wise Mechanick, the naturall Reason, before the Mathematicall, and sensible conceits before abstracted.“, Wotton 1624, 49–50.
„where let me note by the way, that when any thing is Mathematically demonstrated weak, it is much more Mechanically weake: Errors euer occurring more easily in the management of Grosse Materials, then Lineall Designes.“, Wotton 1624, 49–50.
Vgl. Becchi 1999.
„I heare [Wotton] is now retiring to some corner in the countrie to finish a worke he is setting out of the mathematikes or perhaps building of castles in the ayre.“, John Chamberlain, Brief an Dudley Carleton (London, den 31. Januar 1624, n.s.); vgl. Smith 1907, Bd. I, 194.
Was über Wotton geschrieben wurde, gilt auch für Baldi: „Wenig gelesen, wenig verstanden, das bezeichnet wohl das eigentliche Schicksal von Wottons Elements of Architecture – wohl bis auf den heutigen Tag.“, Oechslin 2002, 267.
„sulla resistenza dei corpi ad esser spezzati.“, Galilei 1638.
„Taccia dunque la turba de gli Architetti pratici, se io scriverò di Vitruvio e di Leon Battista, e non di loro, poiché eglino, ornati, come si dice, di tutte l’arme, hanno ragione di militia ne l’essercito de’ Matematici, de’ quali io vo scrivendo le vite. L’istesso dico a’ Mecanici semplicemente pratichi, ancorchè per semplice pratica habbiano fatto meraviglie.“, vgl. Narducci 1886, 464. Diese Passage und insbesondere der Ausdruck „geschmückt, wie man sagt, mit allen Waffen“ sind ein wörtliches Zitat Vitruvs selbst, vgl. Vitruv 1488, Buch I. Zu den Vite de’ matematici siehe auch Baldi 1998.
Silberschlag 1786, Abschnitt 676, 236: „Steinerne Brücken erfordern auch steinerne Gewölbbogen, welche auf den massiven Pfeilern ruhen. Und nun gerathen wir an eine Materie, die mit Recht das Räthsel der Architektur genennet wird. Der erfahrne Nürbergische Architekt Jacob Schübler wünschet in seiner Zimmermanskunst, daß ein jeder, der in dem Geheimnisse der Wölbkunst etwas zuverläßiges gefunden, solches zum Besten des gemeinen Bestens bekannt machen möchte. Dieses ist häufig genug geschehen, demohngeachtet sind wir noch nicht weiter gekommen, als daß wir nunmehr die beste Gewölblinie anzugeben wissen. Zu Ansehung der Breite der Bogen und Stärke der Widerlagen tappen wir noch immer im Finstern herum, und jedweder Architekt ersinnet sich nach seiner Vorstellung, die er sich vom Drucke und Gegendrucke der einzelnen Theile der Wölbung machtet, seine eigene Methode, der er folget.“
„Mr. Hooke represented the mechanical way of making an arch of such a figure, as shall sustain any weight given. Being asked, whether he had ready the demonstration of it, he answered, that he had given it to the president, who was absent from this meeting.“, Birch 1756, 461.
„Dr. Wren delivered to the president his demonstration of what line it is, which an arch, fit to sustain any assigned weight, makes. […] Mr. Hooke being called upon for his demonstration of the same subject answered, that he had already declared the substance of it to the president, who yet desired him to give it also in writing, that so it might be with more leisure and conveniency examined.“, Birch 1756, 465.
„Mr. Hooke produced the representation of the figure of the arch of a cupola for the sustaining such and such determinate weights, and found it to be a cubico-parabolical conoid; adding, that by this figure might be determined all difficulties in architecture about arches and butments.“, Birch 1756, 498.
Vgl. auch Heyman 1998.
„(a decimate of the centesme of the Inventions I intend to publish, though possibly not in the same order, but as I can get opportunity and leasure; most of which, I hope, will be as useful to Mankind, as they are yet unknown and new).“
„2. The true Mathematical and Mechanichal form of all manner of Arches for Building, with the true butment necessary to each of them. A Problem which no Architectonick Writer hath ever yet attempted.“, Hooke 1676, 31. Das Anagramm wird später von Richard Waller (1705, XXI) wie folgt interpretiert: „Ut pendet continuum flexile, sic stabit contiguum rigidum inversum, which is the Linea Catenaria.“ Über dasselbe Thema schreibt Hooke in seinem Tagebuch (am 26. September 1675): „Riddle of arch, of pendet continuum flexile, sic stabit grund Rigidum.“, vgl. Robinson and Adams 1935, 182.
Vgl. für weitere Untersuchungen zu diesem Thema, die auch den grundlegenden Beitrag von Jacob Bernoulli berücksichtigen Truesdell 1960; Benvenuto 1991.
Vgl. Soo 1998; Bolton and Duncan 1942.
„C’est un problème des plus difficiles qu’il y ait dans l’Architecture, que de connoître la force que doivent avoir les pieds droits des voûtes pour en soutenire la poussée, les Architectes n’ont trouvé jusqu’à présent aucune regle certaine pour la déterminer.“, La Hire 1712, 69.
Vgl. Becchi et.al. 2013.
Das Traktat beinhaltet 126 Propositions.
Die Procès-verbaux der Académie d’architecture wurden zwischen 1911 und 1926 in 9 Bänden (zuzüglich eines Indexbandes, gedruckt 1929) von Henry Lemonnier publiziert, vgl. Lemonnier 1911–1929. In jenen Büchern, die ansonsten äusserst gewissenhaft geführt sind, fehlen, bis auf den Titel, jegliche Hinweise zu La Hires mémoire vom 30. Juni 1711, vgl. La Hire 1711. Vielleicht hat Lemonnier diese Handschrift übersehen oder als unwichtig erachtet. In jedem Fall ist sie in den Archiven des Institut de France vorhanden. Eine Transkription von La Hires Beitrages Remarques sur l’époisseur von 1692 ist in Band 2 der Procès-verbaux, S. 345–349, zu finden.
Vgl. zur Geschichte der Académie royale d’architecture Schöller 1993.
Andere Exemplare befinden sich in den folgenden Bibliotheken: Bibliothèque de l’École Nationale des Ponts et Chaussées (Paris), Bibliothèque municipale (Rennes), Bibliothèque municipale (Langres). Vgl. zu diesem Thema Becchi 2002 und Becchi et.al. 2013.
Das Traktat wird erstmals am 20. Oktober 1698 an der Académie d’architecture vorgestellt, vgl. Lemonnier 1911–1929, Bd. 3, 51.
Vgl. Alberti 1485, Buch VII.
Vgl. Becchi 2013b.
Derand 1643. Vgl. Becchi 2010.
„tous les voussoirs ettoient tous poussez vers le centre de la voûte avec un mesme effort“, La Hire 1692.
„car la clef et les voussoirs d’en haut qui en sont proches ne feroient pas plus d’effort que s’ils estoient tous joints ensemble et s’ils ne faisoient qu’un mesme solides, dont il faudroit considérer l’effort comme celui d’une seule pierre toute droite pesant autant que tous les voussoirs ensemble et posée de niveau sur les pieds droits.“, La Hire 1692.
Wie auch Amédée François Frézier wenige Jahre später, vgl. Frézier 1737–1739, Bd. 3, Kap. XII.
„[De La Hire] Vidit aliquid; quid autem viderit, ipse non intelligit.“, Brief an Gottfried Wilhelm Leibniz vom 8. November 1698, vgl. Gerhardt 1855, Brief Nr. 85, 550. Das Zitat bezieht sich auf die Analogie Bogen – Kettenlinie, wie sie in dem Traité de mécanique von La Hire beschrieben wird.
„laquelle devroit servir de base à cette théorie [la poussée des voûtes] importante et qui paroît ignorée de presque tous ceux qui ont travaillé sur cette matière.“, Lemonnier 1911–1929, Bd. 9, 344.
Vgl. Becchi 2006.
Bereits Plinius, in seiner Historia naturalis, hatte deren wunderbare Widerstandsfähigkeit gepriesen, vgl. Plinius Secundus 1832.
