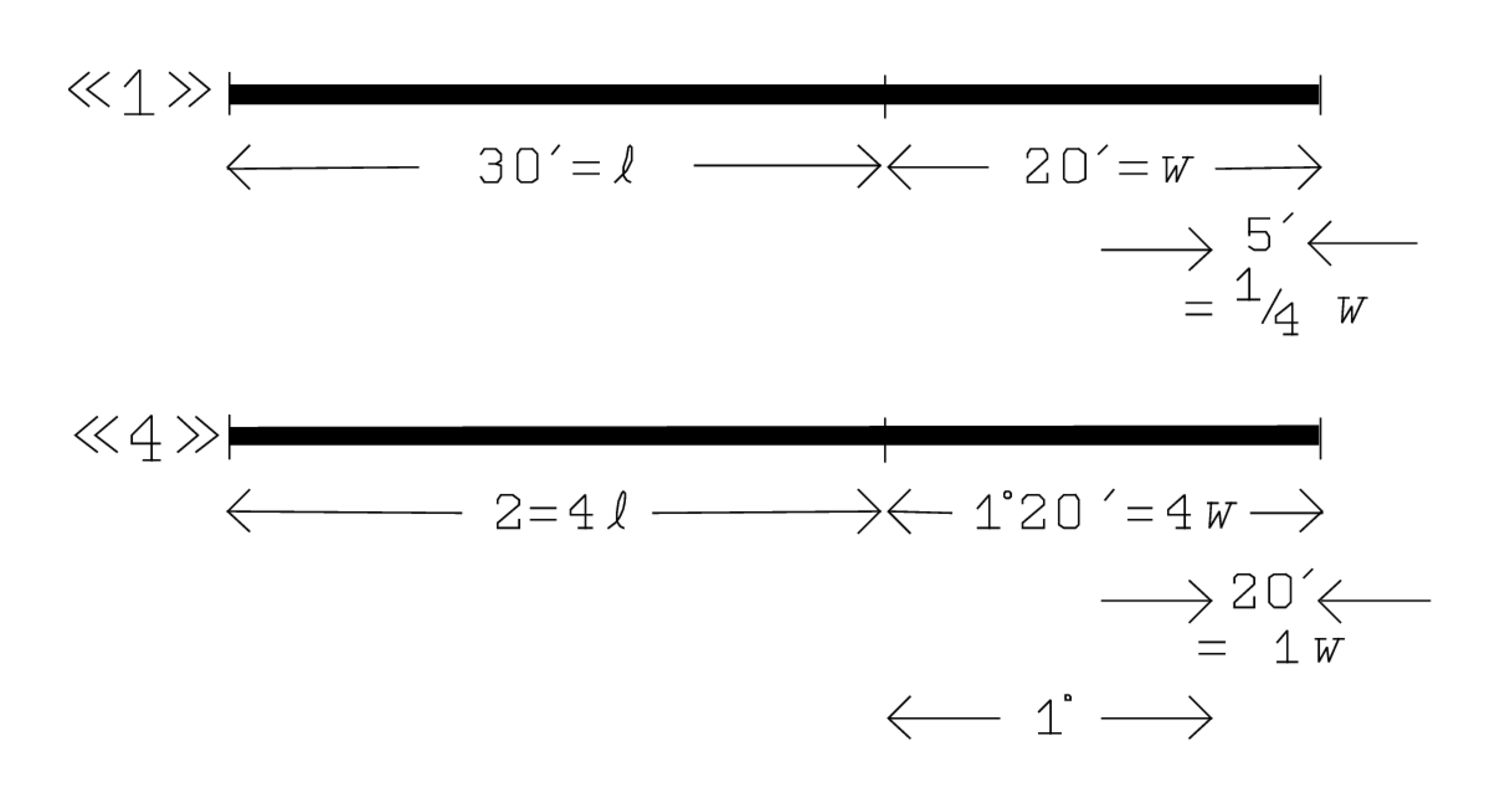Unser Hauptthema wird die Lösung quadratischer Gleichungen in der
altbabylonischen Mathematik sein.1 Weil die Lösung quadratischer Gleichung
aber oft Umformungen linearer Probleme
TMS XVI #1
(1)Den 4ten Teil der Breite habe ich von der Länge und der Breite herausgerissen: 45′. Du, 45′
(2)auf 4 erhöhe, 3 siehst Du. 3, was ist das? 4 und 1 setze,
(3)50′ und 5′, zum Herausreißen, setze. 5′ auf 4 erhöhe, 1 Breite. 20′ auf 4 erhöhe,
(4)1°20′ ⟨siehst⟩ Du,2 4 Breiten. 30′ auf 4 erhöhe, 2 ⟨siehst⟩ Du, 4 Längen. 20′, 1 Breite zum Herausreißen,
(5)von 1°20′, 4 Breiten, reiße heraus, 1 siehst Du. 2, die Länge, und 1, 3 Breiten, häufe an, 3 siehst Du.
(6)igi 4 spalte ab, 15′ siehst Du. 15′ auf 2, Längen, erhöhe, 30′ ⟨siehst⟩ Du, 30′ die Länge.
(7)15′ auf 1 erhöhe, 15′ der Beitrag der Breite. 30′ und 15′ lasse enthalten.
(8)Weil „Das 4tel der Breite, zum Herausreißen“, wie man Dir gesagt hat, von 4, 1 reiße heraus, 3 siehst Du.
(9)igi 4 ⟨spalte⟩ ab, 15′ siehst Du, 15′ auf 3 erhöhe, 45′ ⟨siehst⟩ Du, 45′ so viel wie Breiten.
(10)1, so viel wie Längen, setze. 20, die wahre Breite nimm, 20 auf 1′ erhöhe, 20′ siehst Du.
(11)20′ auf 45′ erhöhe, 15′ siehst Du. 15′ von 3015′ reiße heraus,
(12)30′ siehst Du, 30′ die Länge.
Dieser
Obwohl viele der Ausdrücke, die in der Übersetzung auftauchen, schon im Abschnitt „Eine neue Interpretation“ erklärt wurden, ist es wohl hilfreich, den Text Wort für Wort durchzugehen.
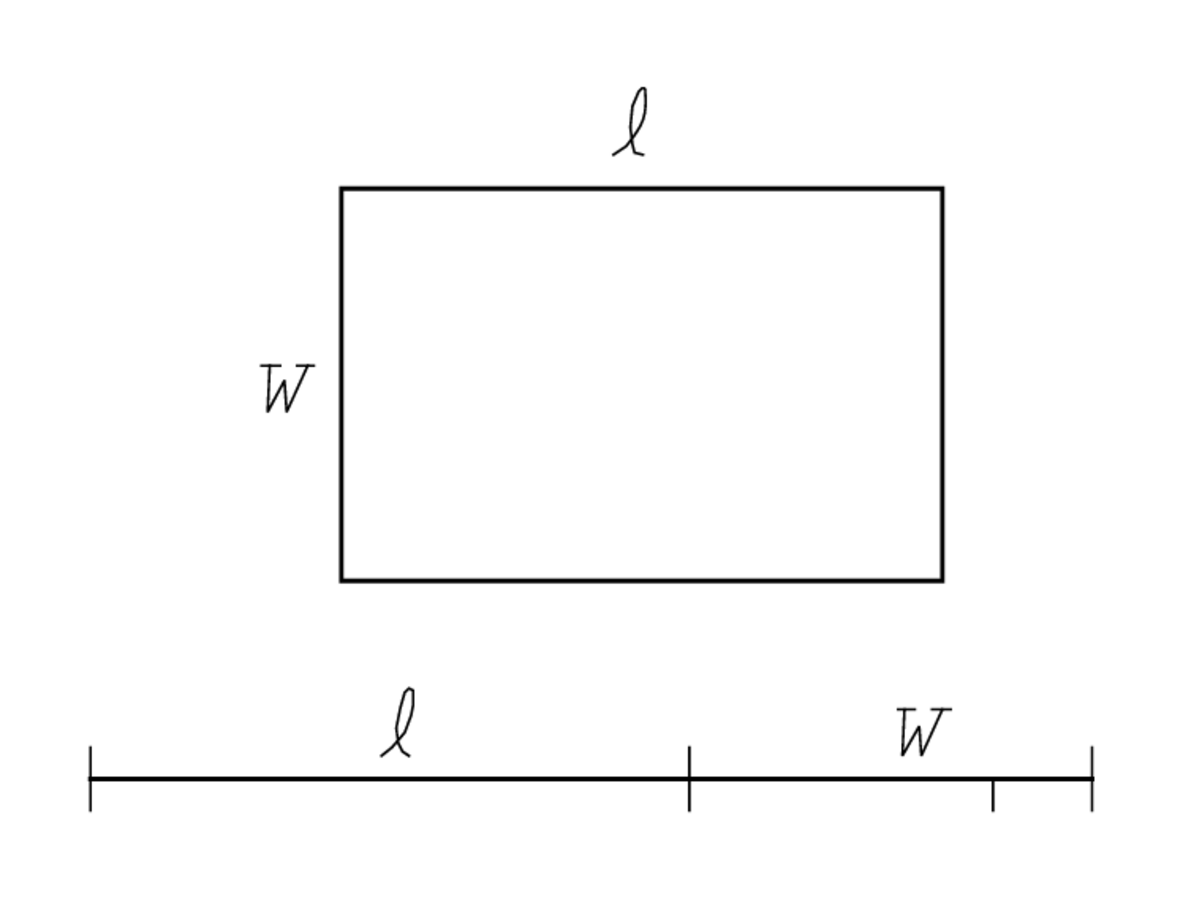
Zeile 1 formuliert eine Gleichung: Das 4tel der Breite, von der Länge und der Breite habe ich herausgerissen, 45′.
Die Gleichung dreht sich also um eine Länge und eine Breite. Dies
bedeutet, dass das Objekt ein Rechteck ist – vom
altbabylonischen Standpunkt aus ist das Rechteck die einfachste Figur,
die nur von einer Länge und einer Breite festgelegt
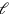 die Länge und
die Länge und
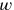 die Breite, dann können
wir die Gleichung in Symbolen so ausdrücken:
die Breite, dann können
wir die Gleichung in Symbolen so ausdrücken:
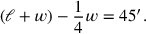
|
Etwas ist jedoch bei dieser Übersetzung verloren gegangen. Tatsächlich
ist die Länge und die Breite ein verkürzter Ausdruck für das
„Anhäufen“,
Sind die Länge und die Breite einmal „angehäuft“, ist es möglich,
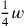 „herauszureißen“,
„herauszureißen“,
Zeile 1 zeigt die Natur einer babylonischen
Als nächstes fordern Zeilen 1 und 2 den Schüler auf, die
45′ (auf der rechten Seite der Version in
moderner Symbolsprache) mit 4 zu multiplizieren:
Du, 45′ auf 4 erhöhe, 3 siehst Du.
„Erhöhen“
Die Antwort zu dieser Frage findet man in Zeilen 2–5.
4 und 1 setze: Zuerst soll der Schüler 4 und 1
„setzen“.
Die Zahl „1“ entspricht der Tatsache, dass die Zahl 45′, die in der ursprünglichen Gleichung rechts steht, ebenso wie die Größen auf der linken Seite alle ein einziges Mal benutzt werden. Die Zahl „4“ wird „gesetzt“; weshalb werden wir gleich sehen, wenn wir erklären was passiert, wenn 45′ und die entsprechenden Größen 4 Mal genommen werden.
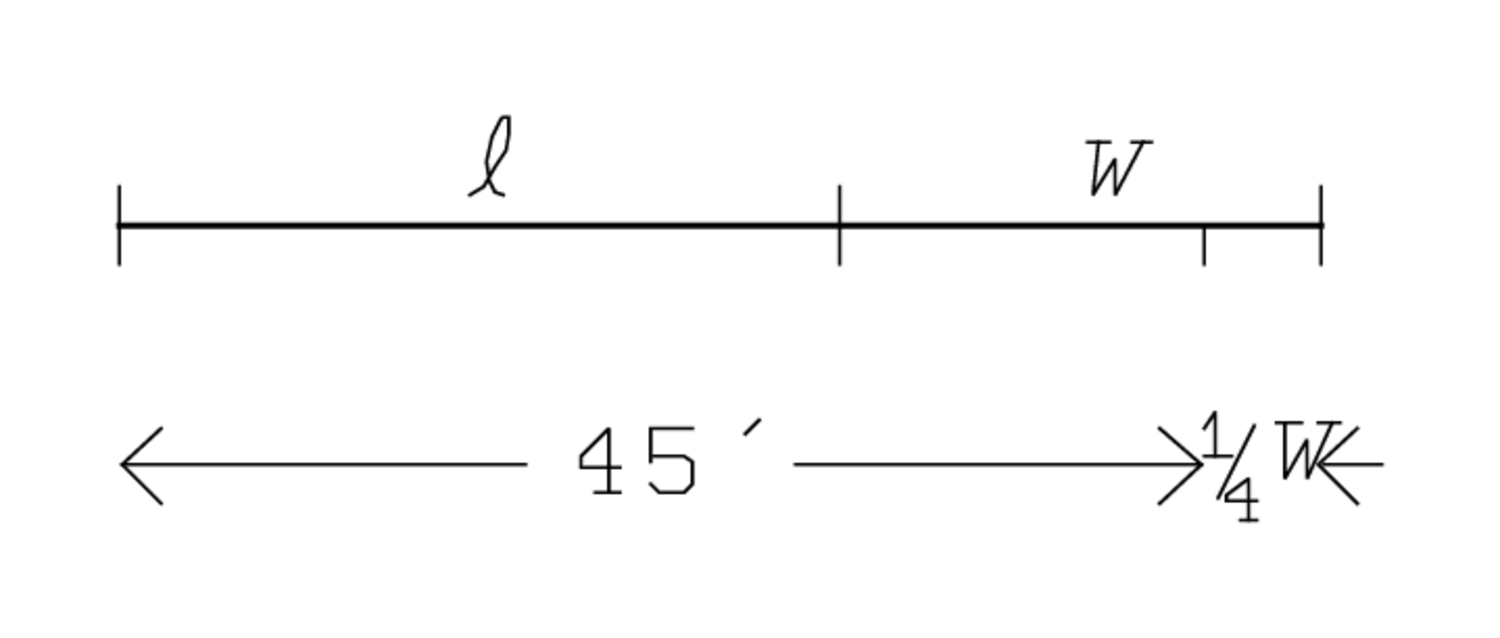
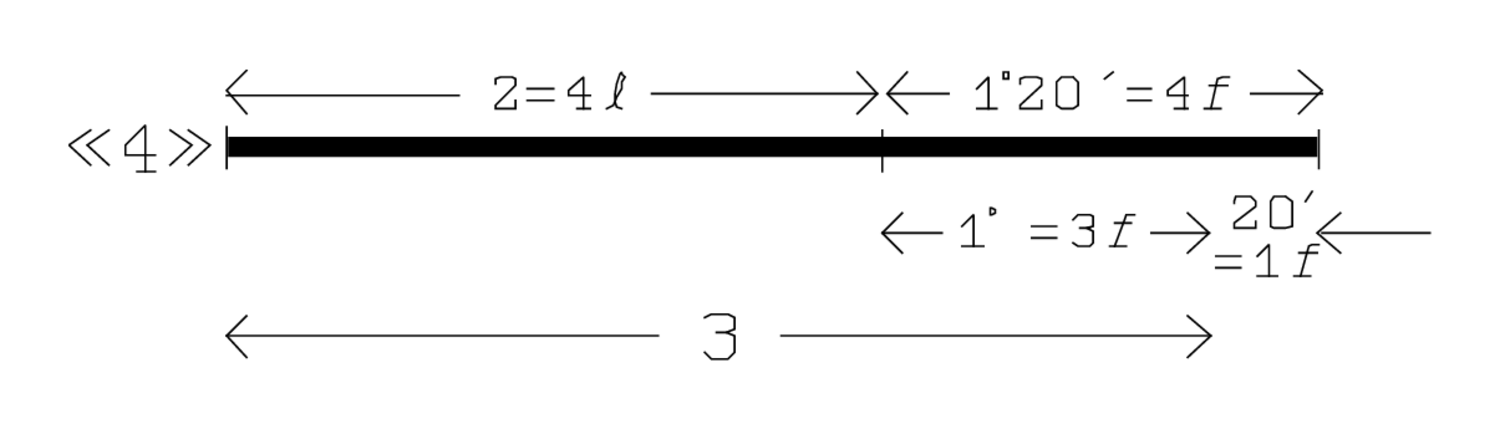
50′ und 5′, zum Herausreißen, setze:
die Zahlen 50′ und 5′ werden auf das Niveau „1“
des Diagramms gesetzt. Dies sollte uns überraschen: es zeigt, dass der Schüler
bereits wissen muss, dass die Breite 20′ und die Länge 30′
ist. Wüsste er das nicht, dann könnte er nicht verstehen, dass
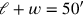 und dass
und dass
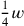 (das, was herausgerissen
werden soll) 5′ ist. Um der Klarheit willen sind in unserem
Diagramm nicht nur die Zahlen 50′ und 5′, sondern
auch 30′ und 20′ auf Niveau „1“
eingezeichnet, obwohl der Text nicht von ihnen spricht.
(das, was herausgerissen
werden soll) 5′ ist. Um der Klarheit willen sind in unserem
Diagramm nicht nur die Zahlen 50′ und 5′, sondern
auch 30′ und 20′ auf Niveau „1“
eingezeichnet, obwohl der Text nicht von ihnen spricht.
Die Zeilen 3–5 zeigen noch überzeugender, dass der Text voraussetzt, dass der Schüler die Lösung des Problems (das also daher nur ein Quasi-Problem ist) bereits kennt. Das Ziel des Textes ist daher nicht, eine Lösung zu finden. Wie bereits gesagt, soll der Text die konzepte und die Verfahren erklären, um die Gleichung zu verstehen und reduzieren zu können.
Diese Zeilen erklären, warum und wie die Ausgangsgleichung
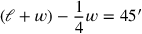
|
durch Multiplikation mit 4 in die Gleichung

|
transformiert wird.
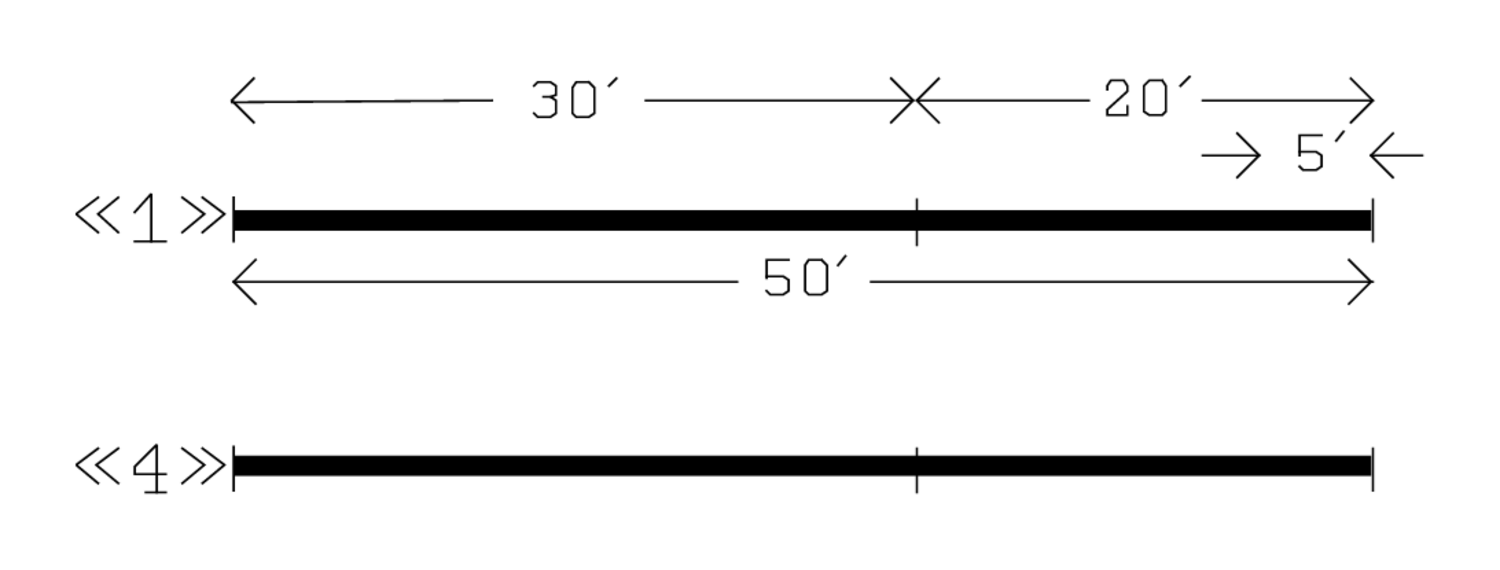
Diese Rechnung kann in Abb. 2.4 verfolgt werden, wo die Zahlen auf dem Niveau „1“ mit 4 multipliziert werden und so diejenigen auf dem Niveau „4“ ergeben:
5′ auf 4 erhöhe, 1 Breite:
5′, also
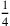 der Breite, wird
mit 4 multipliziert, was 20′ ergibt, also eine Breite.
der Breite, wird
mit 4 multipliziert, was 20′ ergibt, also eine Breite.
20′ auf 4 erhöhe, 1°20′ ⟨siehst⟩ Du, 4 Breiten: 20′, also 1 Breite, wird mit 4 multipliziert, was´ 1°20′ ergibt, also 4 Breiten.
30′ auf 4 erhöhe, 2 ⟨siehst⟩ Du, 4 Längen: 30′, also 1 Länge, wird mit 4 multipliziert. Dies ergibt 2, also 4 Längen.
Nachdem alle Zahlen auf dem Niveau „1“ mit 4 multipliziert worden sind und wir nun die entsprechenden Zahlen auf Niveau „4“ kennen, sagt der Text (Zeilen 4 und 5), was bleibt, wenn 1 Breite von den 4 Breiten eliminiert wird: 20′, 1 Breite, zum Herausreißen, von 1°20′, 4 Breiten, reiße aus, 1 siehst Du
Schließlich werden die individuellen Komponenten der Summe
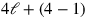
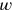 identifiziert, wie in
Abb. 2.5 gezeigt wird:
2, die Längen, und 1, 3 Breiten, häufe an,
3 siehst Du: 2, also 4 Längen, und 1, also
identifiziert, wie in
Abb. 2.5 gezeigt wird:
2, die Längen, und 1, 3 Breiten, häufe an,
3 siehst Du: 2, also 4 Längen, und 1, also
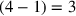 Breiten, werden addiert.
Dies ergibt die Zahl 3.
Wir haben jetzt die Antwort auf die Frage aus Zeile 2 gefunden:
3 siehst Du. 3, was ist das?
Breiten, werden addiert.
Dies ergibt die Zahl 3.
Wir haben jetzt die Antwort auf die Frage aus Zeile 2 gefunden:
3 siehst Du. 3, was ist das?
Aber die Lektion endet hier nicht. Während Zeilen 1–5 erklären, wie die Gleichung
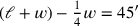 in
in
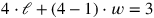 umgewandelt werden kann, führt das, was in Zeilen 6–10 durch eine Division
durch 4 folgt, zu einer Umformung dieser Gleichung in
umgewandelt werden kann, führt das, was in Zeilen 6–10 durch eine Division
durch 4 folgt, zu einer Umformung dieser Gleichung in
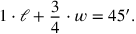
|
Die Babylonier haben Divisionen durch 4 als Multiplikationen mit
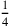 ausgeführt. Daher sagt Zeile 6, dass
ausgeführt. Daher sagt Zeile 6, dass
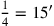 :
igi 4 spalte ab, 15′ siehst Du.
igi 4 kann in der Tabelle
:
igi 4 spalte ab, 15′ siehst Du.
igi 4 kann in der Tabelle
Abb. 2.6 zeigt, dass dies einer Rückkehr auf das Niveau „1“
entspricht:
15′ auf 2, Längen, erhöhe,
30′ ⟨siehst⟩ Du,
30′ die Länge: 2, also 4 Längen, multipliziert mit
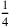 gibt 30′, also 1 Länge.
gibt 30′, also 1 Länge.
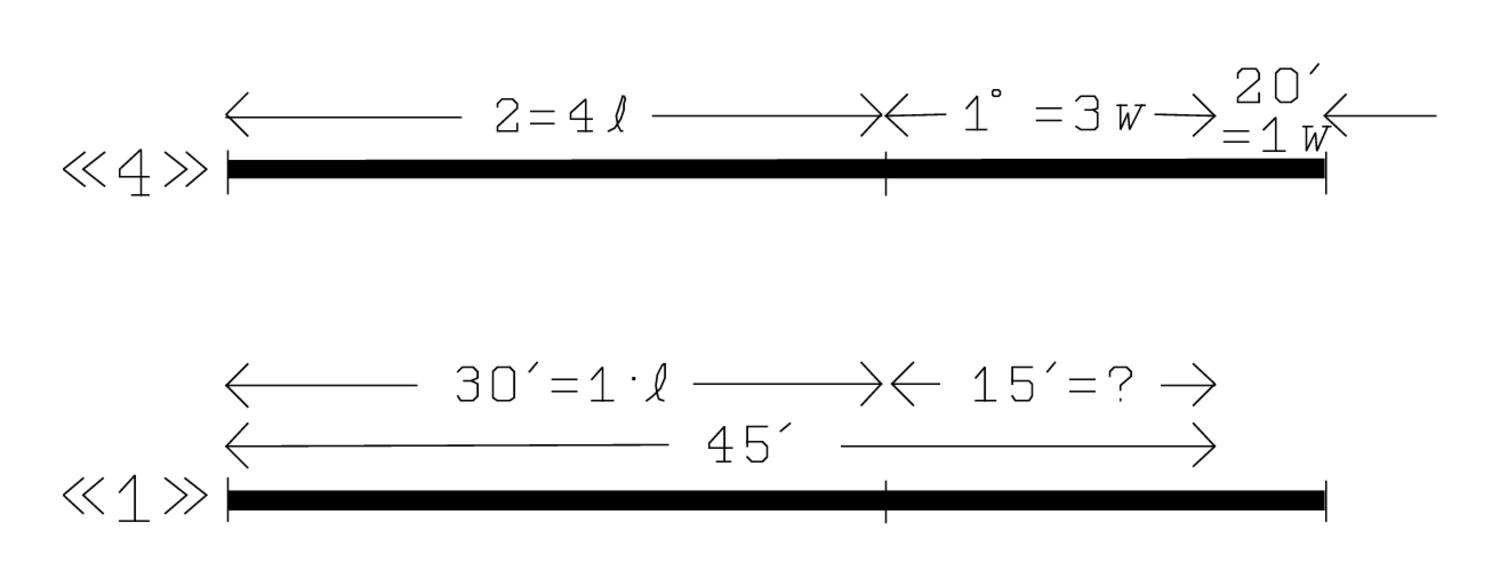
Abb. 2.6: Interpretation von TMS XVI, Zeilen 6–12.
15′ auf 1 erhöhe, 15′ der Beitrag der Breite.
(Zeile 7): 1, also 3 Breiten, multipliziert mit
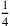 ergibt 15′,
der Beitrag der Breite zur Summe 45′. Die Anzahl der Breiten´, welchem
dieser Beitrag entspricht, wird in Zeilen 8 und 9 bestimmt.
In der Zwischenzeit werden die Beiträge der Länge und der Breite
wiederholt: 30′ und 15′ halte –
eine Abkürzung für möge Dein Kopf halten, wie es in anderen
Texten formuliert wird. Man beachte den Kontrast zur Behandlung der Zahlen
1, 4, 50′ und 5′, die zu Beginn „gesetzt“
wurden.
ergibt 15′,
der Beitrag der Breite zur Summe 45′. Die Anzahl der Breiten´, welchem
dieser Beitrag entspricht, wird in Zeilen 8 und 9 bestimmt.
In der Zwischenzeit werden die Beiträge der Länge und der Breite
wiederholt: 30′ und 15′ halte –
eine Abkürzung für möge Dein Kopf halten, wie es in anderen
Texten formuliert wird. Man beachte den Kontrast zur Behandlung der Zahlen
1, 4, 50′ und 5′, die zu Beginn „gesetzt“
wurden.
Der Beitrag der Breite ist also 15′. Das Ende von Zeile 9
zeigt an, dass die Anzahl der Breiten, welche dem entsprechen –
der Koeffizient der Breite in unserer Sprache – gleich
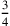 (= 45′) ist: 45′ so viel wie
Breiten. Das Argument dahinter ist bekannt als ein „einfacher
falscher Ansatz“4.
(= 45′) ist: 45′ so viel wie
Breiten. Das Argument dahinter ist bekannt als ein „einfacher
falscher Ansatz“4.
Zeile 8 zitiert die Aufgabenstellung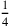 entfernt wird.
entfernt wird.
Der Bequemlichkeit halber wird „gesetzt“, dass die Anzahl
der Breiten 4 ist (dies ist der „falsche Ansatz“).
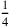 von 4 ist 1 (der Text gibt diese Zahl ohne
Rechnung). Wenn diese eliminiert wird, bleiben 3:
von 4, 1 reiße heraus, 3 siehst Du.
von 4 ist 1 (der Text gibt diese Zahl ohne
Rechnung). Wenn diese eliminiert wird, bleiben 3:
von 4, 1 reiße heraus, 3 siehst Du.
Um zu sehen, welchem Teil der falsch gesetzten 4 diese 3 entspricht,
multiplizieren wir mit
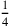 . Obwohl dies bereits in Zeile 6
gesagt wurde, wird in Zeile 9 wiederholt, dass
. Obwohl dies bereits in Zeile 6
gesagt wurde, wird in Zeile 9 wiederholt, dass
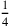 der Zahl
15′ entspricht:
igi 4 ⟨spalte⟩ ab,
15′ siehst Du.
der Zahl
15′ entspricht:
igi 4 ⟨spalte⟩ ab,
15′ siehst Du.
Immer noch in Zeile 9 ergibt die Multiplikation mit 3 den Koeffizienten
der Breite als 45′ (=
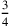 ):
15′ auf 3 erhöhe, 45′
⟨siehst⟩ Du, 45′ so viel wie Breiten.
):
15′ auf 3 erhöhe, 45′
⟨siehst⟩ Du, 45′ so viel wie Breiten.
Ohne Rechnung behauptet Zeile 10, dass der Koeffizient der Länge 1 ist. Wir wissen in der Tat aus Zeile 1, dass eine einzelne Länge zu den 45′ beiträgt, ohne Addition oder Subtraktion. Wir haben daher erklärt, wie die Gleichung
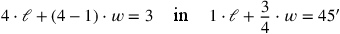
|
umgewandelt wird.
Der Schluss von Zeile 10 gibt uns ein kleines Rätsel: was ist der
Zusammenhang zwischen der „wahren Breite“ und der Breite,
die in den Gleichungen auftaucht?
Die Erklärung könnte die folgende sein: ein richtiges Feld könnte
30 [nindan] auf 20 [nindan] groß sein (ca. 180 m auf 120 m, also
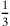 bùr
bùr
Jedenfalls findet man in Zeile 11 wieder, dass die Breite 15′ beiträgt, nämlich durch Multiplikation von 20′ (der Breite) mit dem Koeffizienten 45′: 20′ auf 45′ erhöhe, 15′ siehst Du.
Am Schluss wird der Beitrag der Breite von 45′ eliminiert, das bereits in der Form 3015 geschrieben ist, also als die Summe von 30′ und 15′, in Übereinstimmung mit der Unterteilung, die man sich am Schluss von Zeile 7 gemerkt hat. 30′ bleibt als die Länge: 15′ von 3015′ reiße heraus, 30′ siehst Du, 30′ die Länge.
Alles in allem ist dies eine hübsche pädagogische Erklärung,
Bevor wir den Text hinter uns lassen, verweilen wir noch bei den hier auftretenden Akteure, die auch in den meisten Texten, die ein Problem und das Verfahren zur Lösung beschreiben, auftreten.5 Zum einen beschreibt eine „Stimme“ in der ersten Person Singular die Situation, die er hergestellt hat, und formuliert die Frage. Dann adressiert eine andere Stimme den Schüler und gibt im Imperativ oder in der zweiten Person Singular Präsens Anweisungen; diese Stimme kann nicht mit der ersten identisch sein, die das Problem gestellt hat, weil es diese oft in der dritten Person zitiert, als „weil er gesagt hat“.
In einem schulischen Zusammenhang könnte man sich vorstellen, dass
die Stimme, welche das Problem formuliert, diejenige des Lehrers ist,
und diejenige, welche den Schüler anspricht, die eines Assistenten
– „edubba Texte“6, literarische Texte über die Schule
und das schulische Leben, erwähnen oft einen „älteren Bruder“,
dessen Aufgabe es ist, Anweisungen zu geben. Der Ursprung des Schemas
erscheint aber davon verschieden zu sein. Gewisse Texte aus dem frühen
18. Jahrhundert beginnen mit
„Wenn Dich jemand fragt, ‚ich habe’ ...“.
In diesen Texten ist der Fragesteller
eine hypothetische Person die nicht zu der didaktischen Situation
gehört – ein Vorwand für ein mathematisches Rätsel.
TMS VII #2
Dieser Text ist ziemlich verwickelt. Wer ihn zu undurchschaubar findet, kann ihn erst überspringen und dann hierher zurückkehren, wenn er sich mit der babylonischen Denkart vertraut gemacht hat.
(17)Das Viertel der Breite habe ich zur Länge hinzugefügt; dessen Siebtel
(18)bin ich bis 11 gegangen, über den Haufen
(19)von Länge und Breite ging es 5′ hinaus. Du, setze 4;
(20)7 setze; 11 setze; und 5′ setze.
(21)5′ auf 7 erhöhe, 35′ siehst Du.
(22)30′ und 5′ setze. 5′ auf 11 erhöhe, 55′ siehst Du.
(23)30′, 20′, und 5′, zum Herausreißen, setze. 5′ auf 4
(24)erhöhe, 20′ siehst Du, 20 die Breite. 30′ auf 4 erhöhe:
(25)2 siehst Du, 2, Längen. 20′ aus 20′ reiße heraus.
(26)30′ aus 2 reiße heraus, 1°30′ setze, und 5′ zu ¿50′, dem Haufen von Länge und Breite, füge hinzu?
(27)7 auf 4, vom Viertel, erhöhe, 28 siehst Du.
(28)11, den Haufen aus 28 reiße heraus, 17 siehst Du.
(29)Aus 4, vom Viertel, 1 reiße heraus, 3 siehst Du.
(30)igi 3 spalte ab, 20′ siehst Du. 20′ auf 17 erhöhe,
(31)5°40′ siehst Du, 5°40′, (für) die Länge. 20′ auf 5′, was darüber hinausgeht, erhöhe,
(32)1′40″ siehst Du, 1′40″, was zur Länge hinzugefügt werden soll. 5°40′, (für) die Länge,
(33)von 11, dem Haufen, reiße heraus, 5°20′ siehst Du.
(34)1′40″ zu 5′, was darüber hinausgeht, füge hinzu, 6′40″ siehst Du.
(35)6′40″, was von der Breite herauszureißen ist. 5′, der Schritt,
(36)auf 5°40′, Längen, erhöhe, 28′20″ siehst Du.
(37)1′40″, das von der Länge Hinzuzufügende, zu 28′20″ füge hinzu,
(38)30′ siehst Du, 30′ die Länge. 5′ auf 5°20′
(39)erhöhe: 26′40″ siehst Du. 6′40″,
(40)das aus der Breite Herauszureißende, aus 26′40″ reiße heraus,
(41)20′ siehst Du, 20′ die Breite.
Dies ist das zweite, schwierige Problem einer Tafel. Das erste, leichte (siehe
Seite
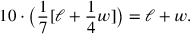
|
Vereinfachen ergibt die Gleichung
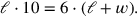
|
Dies ist eine „unbestimmte“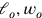 ) gefunden haben, dann kann man alle anderen in der Form
(
) gefunden haben, dann kann man alle anderen in der Form
(
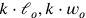 ) schreiben.
) schreiben.
Der Text findet eine Lösung, indem er den ersten Faktor auf der linken
gleich dem ersten Faktor auf der rechten Seite setzt (also
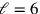 ),
und den zweiten Faktor links gleich dem zweiten Faktor rechts setzt (also
),
und den zweiten Faktor links gleich dem zweiten Faktor rechts setzt (also
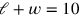 , folglich
, folglich
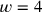 ). Danach erhält man die Lösung,
auf die man von Beginn an stillschweigend gezielt hat, durch „Erhöhen“
auf 5′ (der „Schritt“
). Danach erhält man die Lösung,
auf die man von Beginn an stillschweigend gezielt hat, durch „Erhöhen“
auf 5′ (der „Schritt“
![\frac{1}{7}[ℓ +\frac{1}{4}w]](../../../media/textbooks/3/4/EOAineq_4_28.png) der 10 mal „gegangen“ worden ist). In der Tat: ist
der 10 mal „gegangen“ worden ist). In der Tat: ist
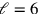 ,
,
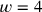 , dann ist der „Schritt“ 1;
wenn wir wollen, dass er 5′ ist (was den üblichen Dimensionen
eines „Schulrechtecks“
, dann ist der „Schritt“ 1;
wenn wir wollen, dass er 5′ ist (was den üblichen Dimensionen
eines „Schulrechtecks“
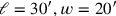 entspricht),
dann muss die Lösung mit diesem Wert multipliziert werden. All dies – und dies
ist nicht offensichtlich – ist nützlich zum Verständnis des zweiten Problems.
entspricht),
dann muss die Lösung mit diesem Wert multipliziert werden. All dies – und dies
ist nicht offensichtlich – ist nützlich zum Verständnis des zweiten Problems.
Das erste Problem ist „homogen“ – alle seine Terme haben
Grad 1 in
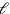 und
und
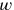 . Das zweite Problem, das wir oben
übersetzt haben, ist inhomogen, und kann in Symbolen wie
folgt ausgedrückt werden:
. Das zweite Problem, das wir oben
übersetzt haben, ist inhomogen, und kann in Symbolen wie
folgt ausgedrückt werden:
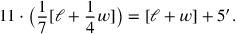
|
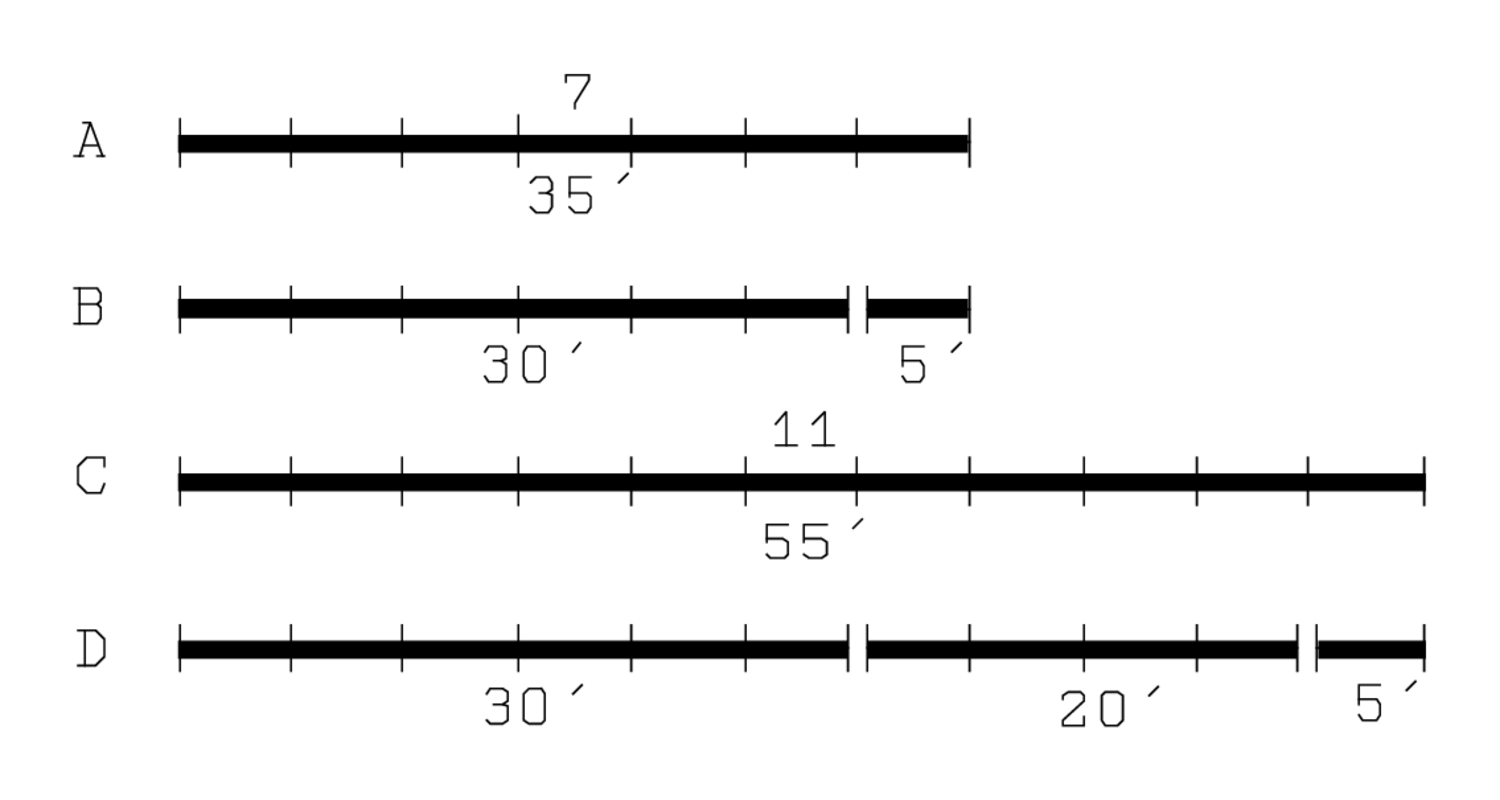
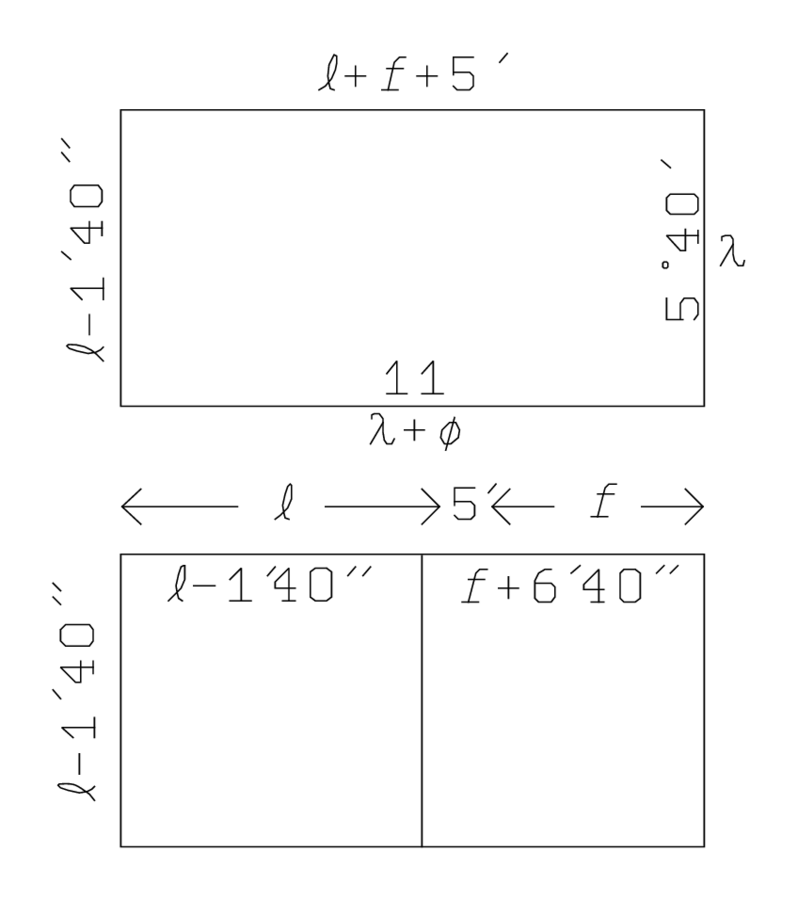
Abb. 2.7: Interpretation von TMS XII, Zeilen 21–23.
Wir bemerken, dass
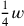 zur Länge „hinzugefügt“ wird;
dass wir
zur Länge „hinzugefügt“ wird;
dass wir
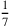 des Ergebnisses nehmen, und dass wir danach
diese Strecke 11 mal “gehen“. Das Ergebnis geht um 5′
über den Haufen von Länge und Breite hinaus. Der Haufen ist also kein Teil
dessen, was sich aus der Wiederholung des Schritts ergibt –
wäre es das, hätte man es „herausreißen“ können.
des Ergebnisses nehmen, und dass wir danach
diese Strecke 11 mal “gehen“. Das Ergebnis geht um 5′
über den Haufen von Länge und Breite hinaus. Der Haufen ist also kein Teil
dessen, was sich aus der Wiederholung des Schritts ergibt –
wäre es das, hätte man es „herausreißen“ können.
Die Lösung beginnt mit einer pädagogischen Erklärung![\frac{1}{7}[ℓ + \frac{1}{4}w]](../../../media/textbooks/3/4/EOAineq_4_36.png) sein muss – das Erhöhen ist eine Verifikation, dass es wirklich das Siebtel ist –
und nicht das „darüber Hinausgehende“ aus Zeile 20. Einmal mehr soll
der Schüler davon ausgehen, dass der Text sich um das Rechteck
sein muss – das Erhöhen ist eine Verifikation, dass es wirklich das Siebtel ist –
und nicht das „darüber Hinausgehende“ aus Zeile 20. Einmal mehr soll
der Schüler davon ausgehen, dass der Text sich um das Rechteck
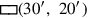 dreht. Mit dieser Figur im
Hinterkopf werden wir der Erklärung der Zeilen 21 bis 23 an der Abbildung
2.7 verfolgen können: wenn der „Schritt“
5′ auf 7 „erhöht“ wird, erhalten wir 35′ (A),
was in
dreht. Mit dieser Figur im
Hinterkopf werden wir der Erklärung der Zeilen 21 bis 23 an der Abbildung
2.7 verfolgen können: wenn der „Schritt“
5′ auf 7 „erhöht“ wird, erhalten wir 35′ (A),
was in
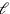 und
und
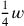 zerlegt werden kann (B).
Wird dies auf 11 „erhöht“, finden wir 55′ (C),
was in
zerlegt werden kann (B).
Wird dies auf 11 „erhöht“, finden wir 55′ (C),
was in
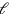 ,
,
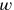 , und 5′ aufgeteilt werden kann (D).
, und 5′ aufgeteilt werden kann (D).
Als nächstes folgt die Vorschrift zur Lösung der Gleichung; diese ist immer noch so formuliert, dass die Lösung als bekannt angenommen wird. „Erhöhen“ auf 4 (Zeilen 23 bis 25) gibt das Äquivalent der folgenden symbolischen Gleichung
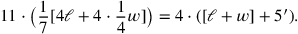
|
Weil der Autor unsere Symbolsprache nicht besitzt, spricht der Text
von
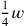 als 5′, findet, dass
als 5′, findet, dass
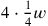 gleich 20′ ist, und identifiziert
dies mit der Breite (Zeile 24); dann erscheint
gleich 20′ ist, und identifiziert
dies mit der Breite (Zeile 24); dann erscheint
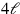 als 2, das die Länge
repräsentieren soll (Zeile 25).
als 2, das die Länge
repräsentieren soll (Zeile 25).
Mittels eines eleganten Tricks, der nicht ganz einfach zu verstehen ist,
wird die Gleichung jetzt homogenisiert. Der Text zerlegt
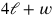 als
als
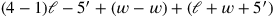
|
und „erhöht“ die ganze Gleichung auf 7. Wir können der Rechnung in moderner symbolischer Übersetzung folgen:
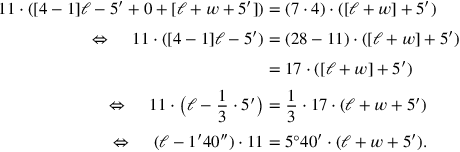
|
Die Babylonier haben allerdings nicht mit solchen Gleichungen gearbeitet;
vermutlich haben sie die Zahlen entlang der Linien einer Zeichnung
(siehe Abb. 2.8) aufgeschrieben. Dies ist der Grund, warum der
„Koeffizient“
 nicht vor Zeile 29 zu erscheinen
braucht.
nicht vor Zeile 29 zu erscheinen
braucht.
Wie im ersten Problem des Texts wird eine Lösung der homogenen
Gleichung durch Identifikation der Faktoren „auf der linken
Seite“ mit denen „auf der rechten Seite“
gefunden (dies ist der Grund, warum die Faktoren auf der linken Seite
der letzten Gleichung invertiert wurden):
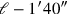 (jetzt „die Länge“ genannt und daher
in Abbildung 2.8 mit
(jetzt „die Länge“ genannt und daher
in Abbildung 2.8 mit
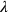 bezeichnet)
entspricht also 5°40′, während
bezeichnet)
entspricht also 5°40′, während
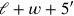 (als der „Haufen“ der neuen Länge
(als der „Haufen“ der neuen Länge
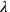 und einer neuen Breite
und einer neuen Breite
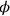 bezeichnet, also
bezeichnet, also
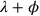 )
ist gleich 11;
)
ist gleich 11;
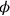 muss daher
muss daher
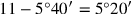 sein.
sein.
Als nächstes bestimmt der Text das „Hinzuzufügende“
(wāṣbum) der Länge, also das,
was zur Länge
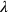 hinzugefügt werden muss, um die
ursprüngliche Länge
hinzugefügt werden muss, um die
ursprüngliche Länge
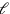 zu erhalten: dies ist gleich
zu erhalten: dies ist gleich
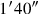 , weil
, weil
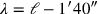 ist. Weiter
findet der Text das „Herauszureißende“ (nāsum)
der Breite, also das, was von der Breite
ist. Weiter
findet der Text das „Herauszureißende“ (nāsum)
der Breite, also das, was von der Breite
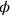 „herausgerissen“ werden muss, um
„herausgerissen“ werden muss, um
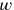 zu erhalten.
Wegen
zu erhalten.
Wegen
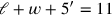 muss
muss
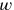 gleich
gleich
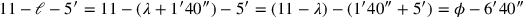 sein; das zu „Herausreißende“ ist also 6′40″.
sein; das zu „Herausreißende“ ist also 6′40″.
Aber das „Hinzufügen“ zu
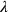 und das
„Herausreißen“ von
und das
„Herausreißen“ von
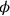 gibt nur eine
mögliche Lösung, nicht die angestrebte. Um die gewünschten
Werte für
gibt nur eine
mögliche Lösung, nicht die angestrebte. Um die gewünschten
Werte für
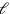 und
und
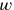 zu erhalten, wird der Schritt
5′ (wie im ersten Problem) auf 5°40′ und
5°20 „erhöht“. Dies ergibt 28′20″ bzw.
26′40″; indem man dem ersten sein „Hinzuzufügendes“
hinzufügt und dem letzteren sein „Herauszureißendes“ herausreißt,
erhalten wir endlich
zu erhalten, wird der Schritt
5′ (wie im ersten Problem) auf 5°40′ und
5°20 „erhöht“. Dies ergibt 28′20″ bzw.
26′40″; indem man dem ersten sein „Hinzuzufügendes“
hinzufügt und dem letzteren sein „Herauszureißendes“ herausreißt,
erhalten wir endlich
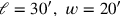 .
.
Wir müssen anerkennen, wie meisterhaft der Autor es versteht, bei seinem
Verfahren die ihm bekannte Lösung zu vermeiden (außer zum Schluss,
wo er den „Schritt“ braucht, um die gewünschte Lösung unter
den unendlich vielen zu produzieren). Die numerischen
Werte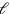 und
und
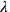 hatten, mussten die Babylonier
Identifizierungen wie „die Länge 30′“ und
„die Länge 5′40″“ benutzen (beides sind Längen,
sodass der Name „Länge“ ohne Zusatz nicht ausreicht).
hatten, mussten die Babylonier
Identifizierungen wie „die Länge 30′“ und
„die Länge 5′40″“ benutzen (beides sind Längen,
sodass der Name „Länge“ ohne Zusatz nicht ausreicht).
Numerische Werte dienen in vielen Texten der Identifizierung; dennoch sind Missverständnisse, die aus einer Verwechslung von gegebenen und lediglich bekannten Zahlen resultieren, sehr selten.
Fußnoten
Wie im Falle der „Algebra“ werden wir vorläufig so tun, als wüssten wir, was mit „Gleichung“ gemeint ist. Eine Untersuchung des vorliegenden Texts wird uns bald erlauben zu verstehen, in welchem Sinn die altbabylonischen Probleme als Gleichungen aufgefasst werden können.
„Du ⟨siehst⟩“ ist die Übersetzung von ta-⟨mar⟩. Der Schreiber lässt also kein Wort aus, sondern benutzt die erste Silbe, (welche die Information über das grammatische Geschlecht enthält) als Logogramm für das ganze Wort. Dies ist in den Texten aus Susa eine übliche Praxis und illustriert, dass die Benutzung von Logogrammen mit der Textart verbunden ist: nur in mathematischen Texten können wir relativ sicher sein, dass kein anderes Verb, das mit der Silbe ta beginnt, an dieser Stelle stehen kann.
Ein rechtwinkliges Dreieck ist ebenso durch eine Länge und eine Breite festgelegt (die beiden Katheten), und diese beiden Größen reichen aus, um es festzulegen (die dritte Seite, wenn sie denn erscheint, kann dann „die lange Seite“ sein). Aber ein Dreieck wird immer als solches eingeführt. Wenn es nicht praktisch rechtwinklig ist, gibt der Text eine Skizze.
Das Wort „praktisch“ ist zu beachten: Die Babylonier hatten kein Konzept eines Winkels als einer messbaren Größe, also nichts, was unserem „Winkel von 78°“ entsprechen würde. Aber sie unterschieden klar zwischen „guten“ und „schlechten“ Winkeln – wie verwenden hier das Wortspiel, dass das Gegenteil eines rechten Winkels ein falscher Winkel war.
Ein rechter Winkel ist einer, dessen Schenkel eine Fläche bestimmen – seien es die Seiten eines rechtwinkligen Dreiecks, die einen rechten Winkel bilden, die Seiten eines Rechtecks, oder die Höhe und die mittlere Grundseite eines rechtwinkligen Trapezes.
„Einfach“ deswegen, weil es auch einen „doppelten falschen Ansatz“ gibt, der zum Lösen komplexerer linearer Probleme benutzt werden kann. Dieser besteht darin, dass man zwei verschiedene Lösungen annimmt, die dann (wie in Legierungsaufgaben) so „gemischt“ werden, dass die beiden Fehler sich herausheben (in moderner Sprache läuft dies auf eine Art lineare Interpolation hinaus). Weil die Babylonier diese Technik nie benutzt haben, bezieht sich „falscher Ansatz“ im Folgenden immer auf den „einfachen falschen Ansatz“.
Das hier vorliegende Dokument benutzt viele Logogramme ohne phonetische oder grammatikalische Ergänzungen. Es ist jedoch genügend in akkadischer Silbenschrift geschrieben, das uns erlaubt, das übliche Schema wahrzunehmen, das folglich auch auf die Übersetzung übertragen ist.
Das sumerische Wort é.dub.ba bedeutet „Tafelhaus“, also „Schule“.