Zeichnungen?
Alle Texte, wie wir oben diskutiert haben, waren mit geometrischen Figuren illustriert. Allerdings finden sich nur auf zwei Tafeln solche geometrischen Figuren, und in beiden Fällen illustrieren sie die Aussage der Aufgabe, nicht aber die Prozedur der Lösung.
Viele Aspekte der Lösungsprozeduren sind in der traditionellen arithmetischen
Interpretation unerklärlich, haben aber eine natürliche Erklärung in der geometrischen
Sichtweise. Es gibt daher gute Gründe anzunehmen, dass bei den Überlegungen der Babylonier
irgendeine Art von Geometrie eine Rolle gespielt haben muss. Es ist allerdings
nicht sehr plausibel, dass die Babylonier Zeichnungen genau wie die unsrigen benutzt haben.
Im Gegenteil legen viele Texte nahe, dass sie sich mit groben strukturellen Diagrammen
zufrieden gegeben haben;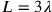 und
und
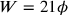 in TMS IX #3
(siehe Seite
in TMS IX #3
(siehe Seite 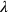 und
und
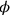 als die Seiten der „Fläche 2“
identifiziert werden konnten.
als die Seiten der „Fläche 2“
identifiziert werden konnten.
Dies ist allerdings wenig überraschend. Wer sich mit altbabylonischen Techniken
auskennt, braucht nur eine grobe Skizze, um den Überlegungen zu folgen; man braucht
die Teilungen und Verschiebungen gar nicht ausführen: die Zeichnung des Rechtecks
genügt bereits, um die verwendete Methode zu verstehen. Ebenso wie wir Rechnungen
im Kopf machen und dabei nur ein oder zwei Zwischenergebnisse notieren, können wir
uns eine „Kopfgeometrie“
Uns ist eine erkleckliche Anzahl von Felderkarten
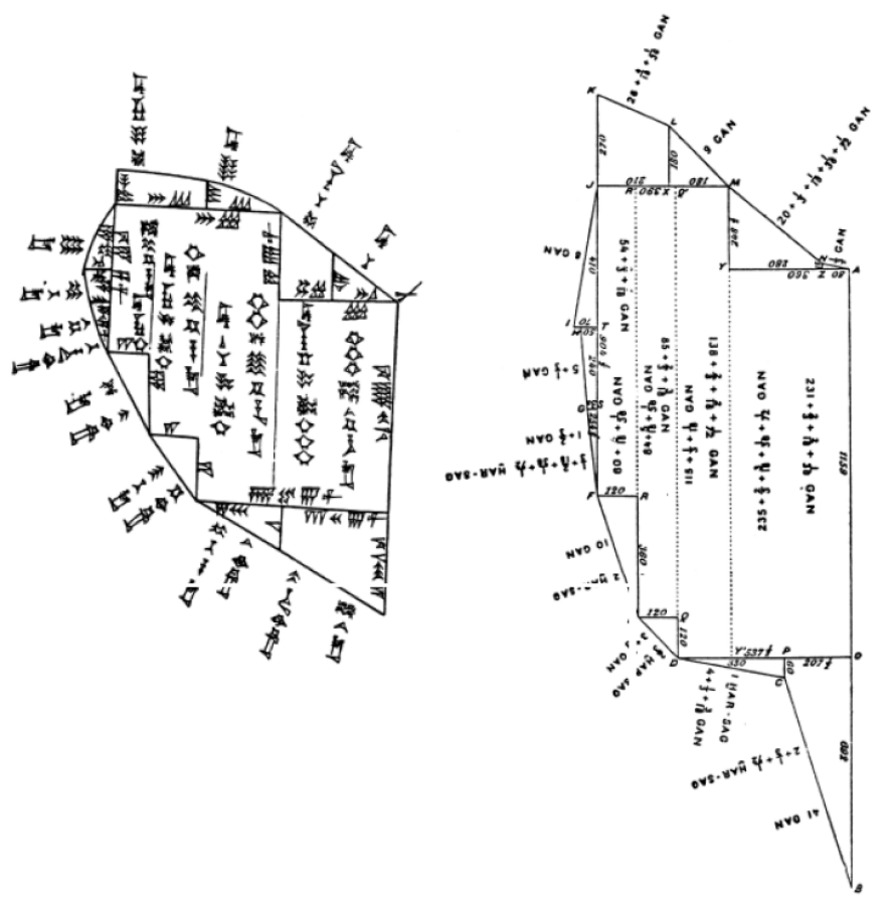
Abb. 6.1: Eine neu-sumerische Felderkarte (21. Jahrhundert v. Chr.), links wie auf der Keilschrifttafel, rechts im korrekten Maßstab nachgezeichnet. Nach F. Thureau-Dangin, “Un cadastre chaldéen”. Revue d’Assyriologie 4 (1897–98), 13–27.
Das Üben der „Kopf-Geometrie“
Staub und Sand dürften auch bei den ersten Schritten des Lernens der Schrift
hilfreich gewesen sein. Aus dieser Einführungsphase kennen wir Tafeln, welche
den Schülern, die sie zum Lernen der Keilschriftsymbole kopieren mussten, als
Vorlage dienten. Aus der nächsten Phase kennen wir ebenfalls
Tontafeln, die von den Schülern geschrieben sind – aber die Arbeit der Schüler
aus der ersten Phase hat keinerlei archäologische Spuren hinterlassen, was bedeutet,
dass diese vermutlich auf Sand oder in den Staub geschrieben worden
sind.
Algebra?
Bis jetzt haben wir, aus Gründen der Bequemlichkeit und in Übereinstimmung
mit der Mehrheit der Mathematikhistoriker, von einer altbabylonischen „Algebra“
gesprochen,
Wir haben inzwischen allerdings eine ganze Reihe von Beobachtungen gemacht, die uns helfen können, eine begründete Meinung zu bilden (und bisweilen anzudeuten, welche Rolle diese Beobachtungen in unserem Argument spielen werden).
Zuerst muss gesagt werden, dass die moderne Algebra, der sich die altbabylonische Technik vielleicht anpassen könnte, eine Technik ist, nämlich der Umgang mit Gleichungen. Nichts in den altbabylonischen Texten erlaubt uns anzunehmen, dass die Babylonier auch nur den Hauch einer algebraischen Theorie besessen haben, wie sie ab dem 16. Jahrhundert entwickelt wurde (betreffend den Zusammenhang zwischen Koeffizienten und den Wurzeln, usw.); wir können a fortiori ihr Vorgehen auch nicht mit dem gleichsetzen, was heutige Mathematiker Algebra nennen (Gruppentheorie und alles, was darauf aufbaut oder dieses Gebiet erweitert). Die heutige Algebra, an welche wir denken sollten, ist diejenige aus dem Schulunterricht, die in Gleichungen ausgedrückt wird.
Wir haben oben gesehen (Seite
Es gibt allerdings einen Unterschied. Ein heutiger Ingenieur arbeitet mit diesen Gleichungen: er schiebt die Größen von einer Seite auf die andere, multipliziert die Koeffizienten, er integriert Funktionen usw. – all diese Dinge existieren nur als Elemente der Gleichungen und haben keine andere Darstellung. Die Operationen der Babylonier dagegen wurden, wie wir gesehen haben, mit Hilfe einer anderen Darstellung realisiert, nämlich durch geometrische Größen2.
Bis auf wenige Ausnahmen (von denen wir oben keine gesehen haben) sind altbabylonische
Lösungen analytisch
Die heutige Algebra der Gleichungen besitzt eine neutrale
„fundamentale Darstellung“
Die heutige Algebra der Gleichungen ist also eine Technik, die Lösung zu finden mittels der Vorstellung, dass wir diese bereits gefunden haben (Analyse), gefolgt von der Manipulation unbekannter Größen, als ob diese bekannt wären – alles innerhalb der funktional leeren Darstellung des Bereichs der abstrakten Zahlen. Ersetzen wir Zahlen durch messbare geometrische Größen, dann können wir dasselbe über die altbabylonische Technik sagen – mit einer kleinen Einschränkung, auf die wir gleich zurückkommen werden. Wenn wir die moderne Technik als eine „Algebra“ verstehen, trotz der riesigen konzeptuellen Entfernung von der Gruppentheorie und ihren Nachkommen, dann erscheint es angemessen, auch die altbabylonische Technik, wie wir sie in den Kapiteln 2-4 angetroffen haben, unter demselben Stichwort zu verbuchen.
Dies bedeutet nicht, dass es keine Unterschiede gibt: es gibt sie, und zwar wichtige; aber diese sind nicht von der Art, wie man sie normalerweise benutzt, um „Algebra“ von anderen mathematischen Gebieten zu trennen.
Neben der Darstellung
Mit dieser Art von Algebra sind wir heute sehr vertraut. Sie erlaubt Lehrern und Lehrbuchautoren, Probleme für Schüler zu konstruieren, bei denen sie sicher sein können, das eine vernünftige Lösung existiert. Der Unterschied ist, dass unsere künstlichen Probleme den Schülern Techniken antrainieren sollen, die ihnen später in realitätsnahen Problemen nützlich sind.
Was wir nicht kennen ist die Offenheit, mit welcher gewisse altbabylonische Texte
vom Wert der Größen sprechen, die im Prinzip als unbekannt
gelten. ,
,
 und
und
 unserer Algebra und der
„Strecke
unserer Algebra und der
„Strecke
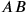 “ unserer Geometrie.
“ unserer Geometrie.
Weil die Texte „Handbücher für Lehrer“ sind, trotz der Anrede „Du“,
die sich an Schüler richtet, können wir nicht ausschließen, dass der Lehrer beim
mündlichen Vortrag der Aufgabe nicht mit dem Finger auf das Diagramm gezeigt und
„diese Breite hier“ oder „diese Fläche dort“ gesagt hat.
Wir können auch nicht behaupten, dass es so gelaufen ist – wir haben kein
besseres Fenster auf die didaktische Praxis der altbabylonischen Mathematik als
das, was uns TMS XVI #1 (Seite
Fußnoten
Das griechische Wort für den Abakus, αβαξ, hat phönizische Wurzeln und bedeutet ursprünglich „Staub“ und „wegfliegen“.
Lediglich einige Transformationen ersten Grades wie diejenigen auf TMS XVI #1 und TMS IX #3 können teilweise als Ausnahmen betrachtet werden; TMS XVI #1 erklärt in der Tat, wie Operationen direkt auf den Wörtern der Gleichung innerhalb der geometrischen Darstellung verstanden werden können. Hat man dies erst einmal verstanden, dann könnte TMS IX #3 vermutlich direkt auf der Ebene der Wörter operieren. Aber TMS XVI #1 ist keine Lösung einer Aufgabe, und in TMS IX #3 ist die Transformation ersten Grades den geometrischen Operationen untergeordnet.
Siehe TMS XVI #2
Zeile 16 und TMS VII #1 Zeile 4
(unten Seite
